In an organ pipe whose one end is at x =0, the pressureis expressed by P=P0cos3πx2sin300πt where x is in meter and t in sec. The organ pipe can be :-
Closed at one end, open at another with length 0.5 m =
Open at both ends, length = 1 m
Closed at both ends, length 2 m
Closed at end, open at another with length 23m
The correct Answer is:C
To determine the type of organ pipe based on the given pressure equation, we will analyze the pressure at different positions along the pipe. The pressure is given by:
P=P0cos(3πx2)sin(300πt)
where x is in meters and t is in seconds.
1. Identify the Closed End:
- The closed end of the organ pipe will have maximum pressure, which occurs when the cosine term is equal to 1.
- Substitute x=0 into the pressure equation:
P=P0cos(3π⋅02)sin(300πt)=P0cos(0)sin(300πt)=P0⋅1⋅sin(300πt)
- Since cos(0)=1, the pressure is maximum at x=0.
2. Check the Open End:
- The open end of the organ pipe will have minimum pressure, which occurs when the cosine term is equal to 0.
- Substitute x=1 into the pressure equation:
P=P0cos(3π⋅12)sin(300πt)=P0cos(3π2)sin(300πt)
- Since cos(3π2)=0, the pressure is minimum at x=1.
3. Check for Maximum Pressure Again:
- Now, check at x=2:
P=P0cos(3π⋅22)sin(300πt)=P0cos(3π)sin(300πt)
- Since cos(3π)=−1, the pressure is maximum (but negative) at x=2.
4. Conclusion:
- We have found that at x=0 (closed end), the pressure is maximum, and at x=1 (open end), the pressure is minimum. At x=2, the pressure is also maximum (but negative).
- This indicates that the organ pipe is closed at both ends.
Final Answer:
The organ pipe can be classified as a closed organ pipe.
- The closed end of the organ pipe will have maximum pressure, which occurs when the cosine term is equal to 1.
- Substitute x=0 into the pressure equation:
P=P0cos(3π⋅02)sin(300πt)=P0cos(0)sin(300πt)=P0⋅1⋅sin(300πt)
- Since cos(0)=1, the pressure is maximum at x=0.
- The open end of the organ pipe will have minimum pressure, which occurs when the cosine term is equal to 0.
- Substitute x=1 into the pressure equation:
P=P0cos(3π⋅12)sin(300πt)=P0cos(3π2)sin(300πt)
- Since cos(3π2)=0, the pressure is minimum at x=1.
- Now, check at x=2:
P=P0cos(3π⋅22)sin(300πt)=P0cos(3π)sin(300πt)
- Since cos(3π)=−1, the pressure is maximum (but negative) at x=2.
- We have found that at x=0 (closed end), the pressure is maximum, and at x=1 (open end), the pressure is minimum. At x=2, the pressure is also maximum (but negative).
- This indicates that the organ pipe is closed at both ends.
The organ pipe can be classified as a closed organ pipe.
Similar Questions
The equation of a stationary wave is y=0.8cos(πx20)sin200πt where x is in cm and t is in s. The separation between consecutive nodes will be
View SolutionThe equation of a stationary wave is y=0.8cos(πx20)sin200πt where x is in cm and t is in s. The separation between consecutive nodes will be
View SolutionA wave is represented by the equation y=Asin(10πx+15πt+π6) wher x is in metre and t in second. The expression represents
View SolutionA wave is represented by the equation :y=Asin(10πx+15πt+π/3) where, x is in metre and t is in second. The expression represents.
View SolutionThe wave described by y =0.25sin(10πx−2πt) where x and y are in meters and t in seconds , is a wave travelling along the
View SolutionThe coordinates of a particle moving in a plane are given by x (t) = a cos (pt) and y (t) = b sin (pt), where a, b (< a), and p are positive constants of appropriate dimensions. Then:
View SolutionA wave disturbance in a medium is described by Y=0.02cos(50πt+π2)cosπx . Where x and y are in m and t in sec. The values in Column-II are in SI units.
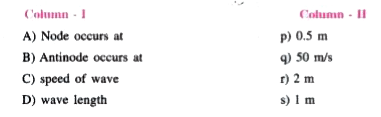
View SolutionA transverse wave propagating along x-axis is represented as y(x,t)=0.8sin(π4−4πt−π2x)where x is in meter and t is in second. The velocity of wave is
View SolutionA transverse wave travelling on a taut string is represented by:
Y=0.01sin2π(10t−x)
Y and x are in meters and t in seconds. Then,
View SolutionA particle is subjected to two simple harmonic motions given by
x1=2.0sin(100πt) and x2=2.0sin(120πt+π/3)
where, x is in cm and t in second. Find the displacement of the particle at
(a) t=0.0125,
(b) t=0.025.
View Solution
