What is the value of frequency at which electromagnetic wave must be propagated for the D - region of atmosphere to have a refractive index of 0.5. Electron density for D - region is 400 electrons/c.c.
200 kHz
104.2 kHz
208.4 kHz
312.6 kHz
The correct Answer is:C
To find the frequency at which an electromagnetic wave must be propagated for the D-region of the atmosphere to have a refractive index of 0.5, we can follow these steps:
1. Understand the Given Values:
- Refractive index (n) = 0.5
- Electron density (N) = 400 electrons/cm³ = 400 × 10^6 electrons/m³ (since 1 cm³ = 10^-6 m³)
2. Use the Refractive Index Formula:
The relationship between the refractive index (n) and electron density (N) in the D-region can be expressed as:
n2=1−81.45⋅Nf2
where f is the frequency in Hz.
3. Substitute the Values:
Substitute n=0.5 and N=400×106 into the equation:
(0.5)2=1−81.45⋅(400×106)f2
4. Calculate n2:
0.25=1−81.45⋅(400×106)f2
5. Rearrange the Equation:
81.45⋅(400×106)f2=1−0.25
81.45⋅(400×106)f2=0.75
6. Solve for f2:
f2=81.45⋅(400×106)0.75
7. Calculate the Right Side:
f2=81.45⋅400⋅1060.75
f2=32.58×1060.75≈4.344×108
8. Take the Square Root:
f=√4.344×108≈208.42×103 Hz=208.42 kHz
Final Answer:
The frequency at which the electromagnetic wave must be propagated is approximately 208.42 kHz.
- Refractive index (n) = 0.5
- Electron density (N) = 400 electrons/cm³ = 400 × 10^6 electrons/m³ (since 1 cm³ = 10^-6 m³)
The relationship between the refractive index (n) and electron density (N) in the D-region can be expressed as:
n2=1−81.45⋅Nf2
where f is the frequency in Hz.
Substitute n=0.5 and N=400×106 into the equation:
(0.5)2=1−81.45⋅(400×106)f2
0.25=1−81.45⋅(400×106)f2
81.45⋅(400×106)f2=1−0.25
81.45⋅(400×106)f2=0.75
f2=81.45⋅(400×106)0.75
f2=81.45⋅400⋅1060.75
f2=32.58×1060.75≈4.344×108
f=√4.344×108≈208.42×103 Hz=208.42 kHz
The frequency at which the electromagnetic wave must be propagated is approximately 208.42 kHz.
Similar Questions
A sky wave with a frequency 55 MHz is incident on D-region of the earth.s atmosphere at 45∘. The angle of refraction is (electron density for D-region is 400 electron/c.c)
View Solutionplane waves refracted for air to water using Huygen.s principal a,b,c,d,e ae length on the diagram.The refractive index of water wrt air is the ratio.

View SolutionCalculated the phase velocity of electromagnetic wave having electron density and frequency for D-layer : (N = 400 electrion/cc and v = 300 kHz)
View SolutionMatch the following elements of column I with their property given in column II.

View SolutionWhich of the following pairs of d-orbitals will have electron density along the axes ?
View SolutionWhich of the following species must have maximum number of electrons in 'dxy' orbital?
View SolutionWhich of the following species must have maximum number of electrons in 'dxy' orbital?
View SolutionFigure shown plane waves refracted for air to water using Huygen.s principle a,b,c,d ,e are lengths on the diagram . The ratio of refractive index of water w.r.t air is
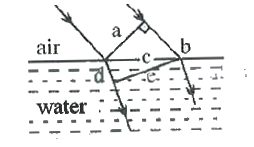
View SolutionTotal number of elements of 5th period which have one or more than one 5d electrons :-
View SolutionFor which subatomic particle the ratio of charge and mass would be greater. (A) Proton, (B) Alpha particle, (C) Neutron, (D) Electron
View Solution
