In a photoelectric experiment , the stopping potential Vs is plotted against the frequency v of the incident light . The resulting curve is a straight line which makes an angle θ with the v - axis. Then tanθ will be equal to (Here E0 = work function of the surface_
he
eh
−ϕe
ehϕ
The correct Answer is:A
To solve the problem, we need to analyze the relationship between the stopping potential Vs and the frequency ν of the incident light in a photoelectric experiment.
1. Understanding the Photoelectric Effect:
The photoelectric effect can be described by the equation:
E=ϕ+eVs
where:
- E is the energy of the incident photons,
- ϕ is the work function of the material,
- e is the charge of the electron,
- Vs is the stopping potential.
2. Relating Photon Energy to Frequency:
The energy of the incident photons can also be expressed in terms of frequency:
E=hν
where h is Planck's constant and ν is the frequency of the incident light.
3. Substituting Energy in the Equation:
By substituting E in the photoelectric equation, we get:
hν=ϕ+eVs
4. Rearranging the Equation:
Rearranging the equation gives:
eVs=hν−ϕ
or,
Vs=heν−ϕe
5. Identifying the Linear Relationship:
The equation Vs=heν−ϕe is in the form of a linear equation y=mx+c, where:
- y is Vs,
- x is ν,
- m (the slope) is he,
- c (the y-intercept) is −ϕe.
6. Finding the Slope:
The slope of the line, which is tanθ (where θ is the angle the line makes with the x-axis), is given by:
tanθ=he
Final Answer:
Thus, the value of tanθ is:
tanθ=he
The photoelectric effect can be described by the equation:
E=ϕ+eVs
where:
- E is the energy of the incident photons,
- ϕ is the work function of the material,
- e is the charge of the electron,
- Vs is the stopping potential.
The energy of the incident photons can also be expressed in terms of frequency:
E=hν
where h is Planck's constant and ν is the frequency of the incident light.
By substituting E in the photoelectric equation, we get:
hν=ϕ+eVs
Rearranging the equation gives:
eVs=hν−ϕ
or,
Vs=heν−ϕe
The equation Vs=heν−ϕe is in the form of a linear equation y=mx+c, where:
- y is Vs,
- x is ν,
- m (the slope) is he,
- c (the y-intercept) is −ϕe.
The slope of the line, which is tanθ (where θ is the angle the line makes with the x-axis), is given by:
tanθ=he
Thus, the value of tanθ is:
tanθ=he
Similar Questions
Knowledge Check
In a photoelectric experiment, the graph of frequency v of incident light (in Hz) and stopping potential V (in V) is as shown in the figure. Planck's constant is (e is the elementary charge)
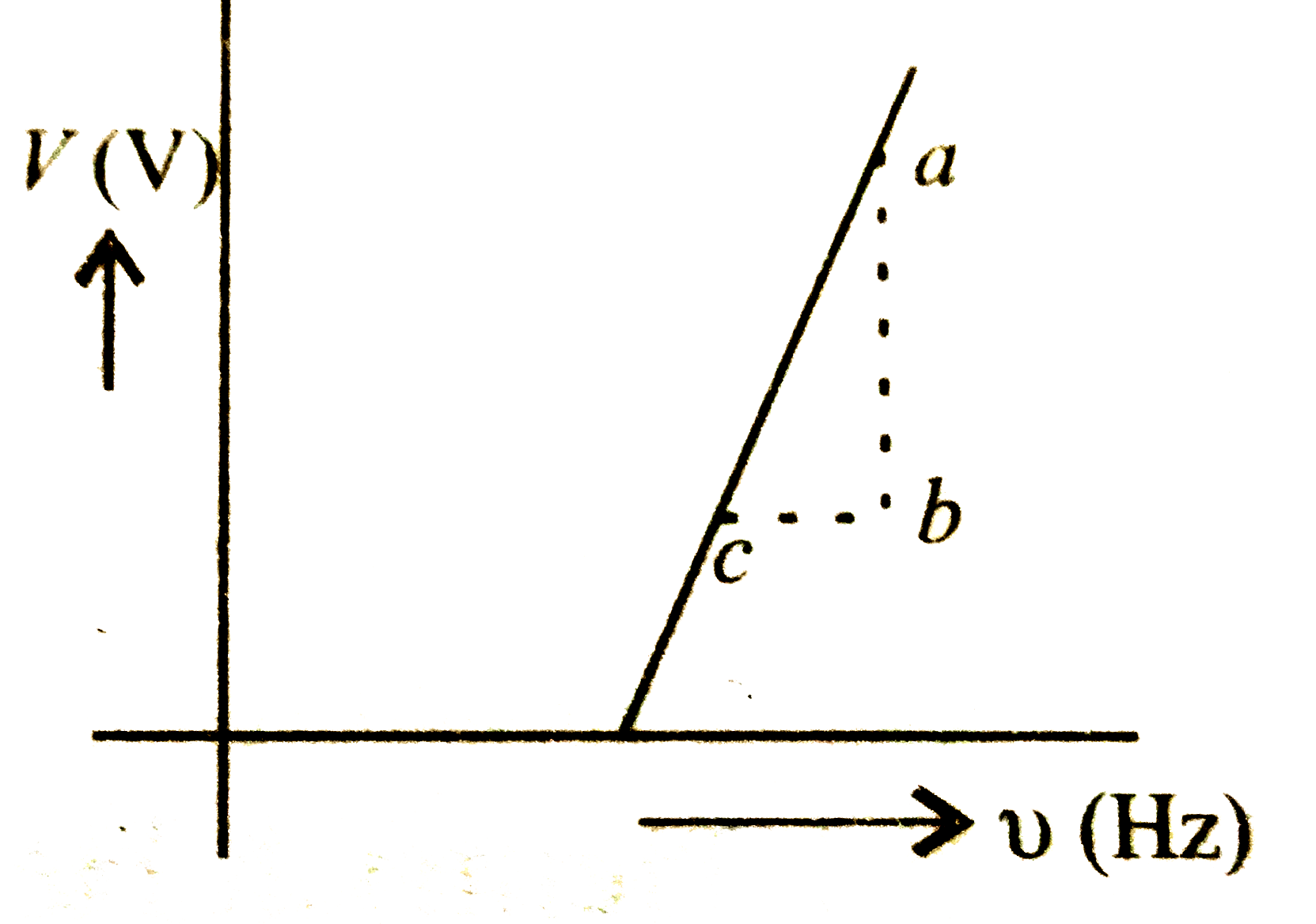 AeabbcBecbacCeacbcDeacab
AeabbcBecbacCeacbcDeacabThe work function of Cs is 2.14 ev find the wavelength of the incident light if the stopping potential is 0.6 V.
A326 nmB454 nmC524 nmD232 nm
In a photoelectric experiment, kinetic energy of photoelectrons was plotted against the frequency of incident radition (v), as show in figure. Which of the following statements is correct ?
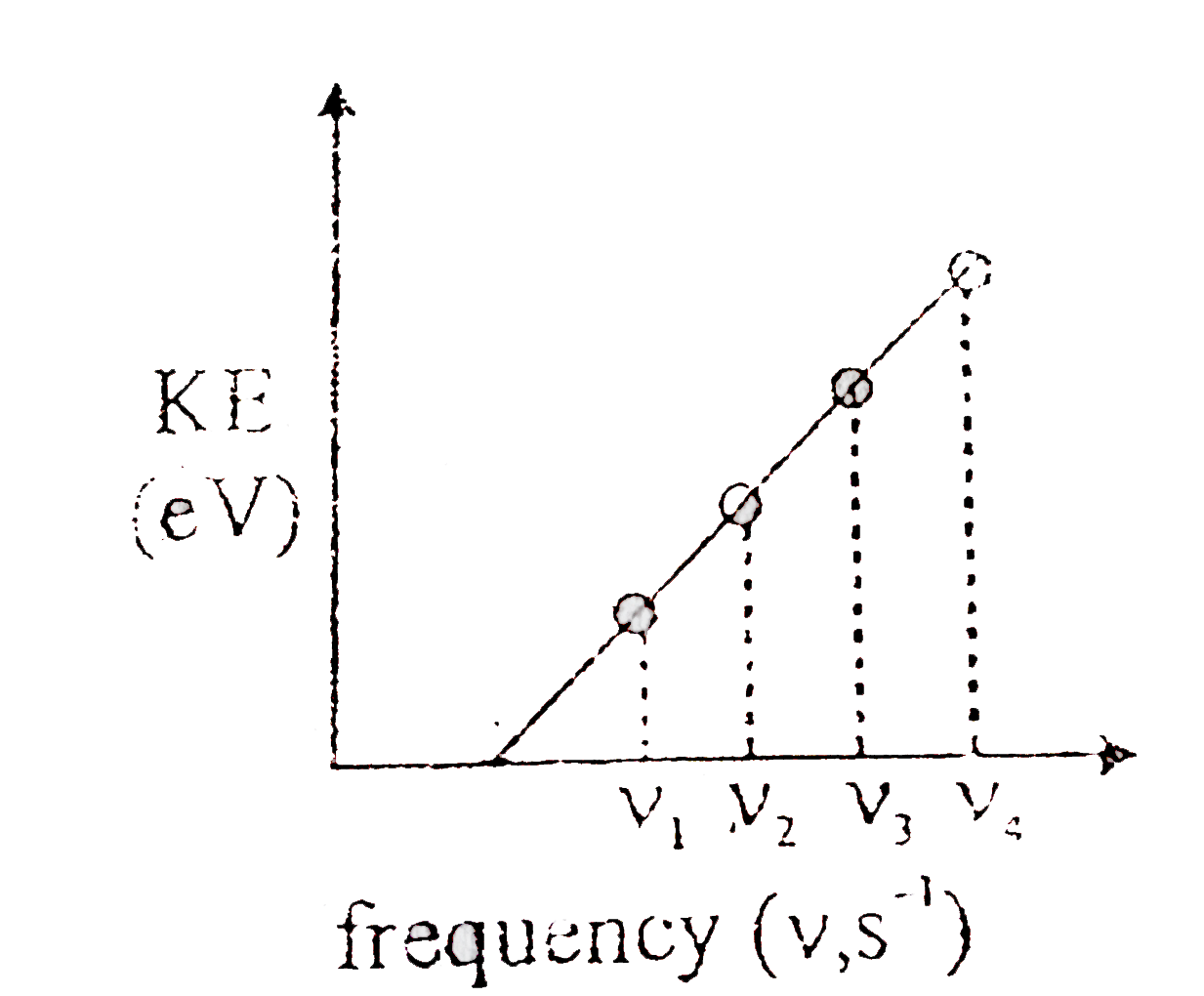
View Solution(i) Plot a labelled graph of |Vs| where Vs is stopping potential versus frequency f of the incident radiation.
(ii) State how will you use this graph to determine the value of Planck.s constant.
View SolutionThe stopping potential V for photoelectric emission from a metal surface is plotted along Y - axis and frequency v of incident light along X - axis . A straight line is obtained as shown . Planck's constant is given by
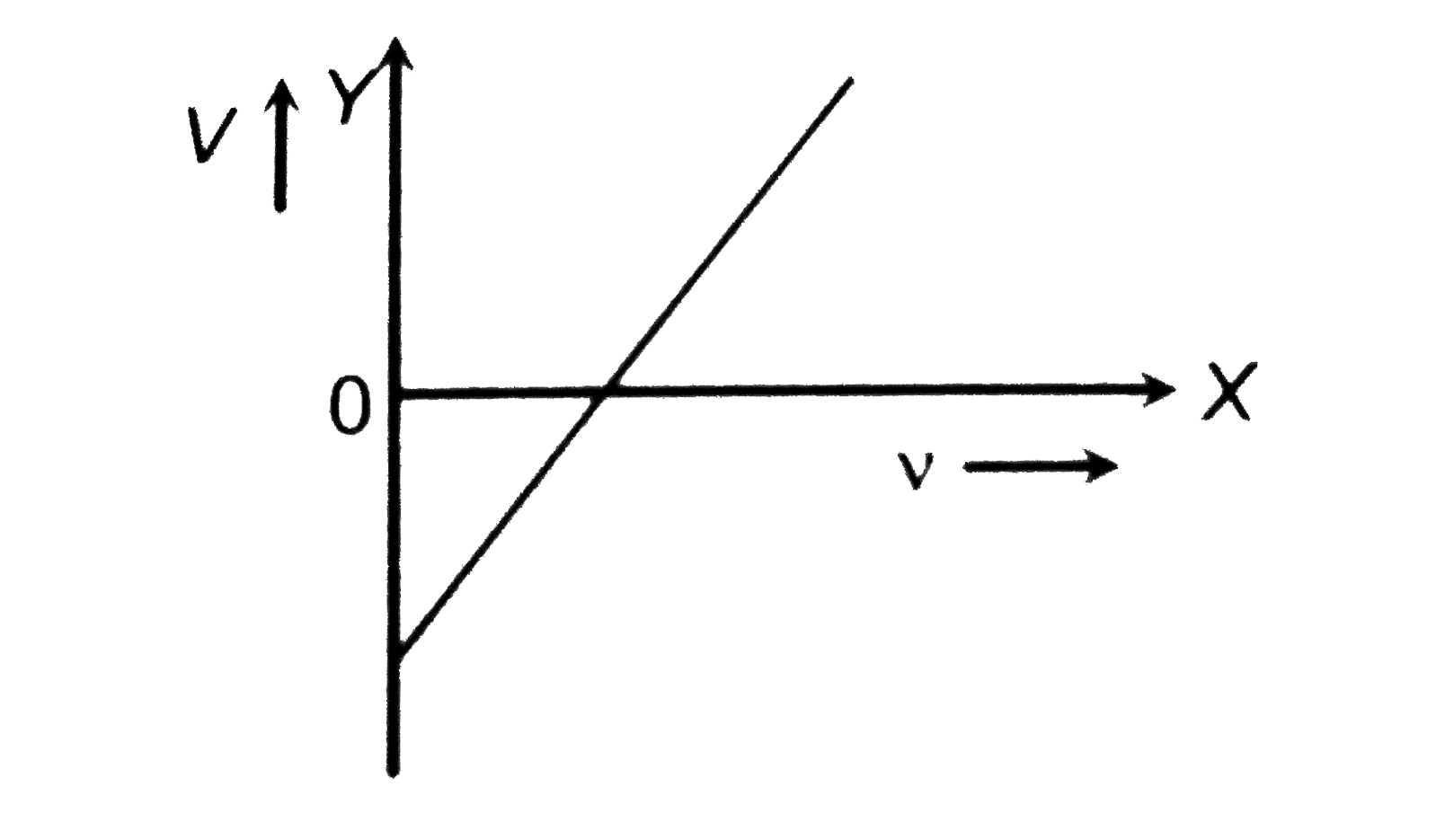
View Solution
The stopping potential V for photoelectric emission from a metal surface is plotted along Y - axis and frequency v of incident light along X - axis . A straight line is obtained as shown . Planck's constant is given by
View SolutionRepresenting the stopping potential V along y-axis and (1λ) along x-axis for a given photocathode, the curve is a straight line, the slope of which is equal to
View SolutionIn a photoelectric experiment, it was found that the stopping potential decreases from 1.85 V to 0.82 V as the wavelength of the incident light is varied from 300nm to 400nm. Calculate the value of the Planck constant from these data.
View Solution

_S01_084_Q01.png)
