1 g of .79Au198(t1/2=65h) gives stable mercury by β− emission. What amount of mercury will left 260 h?
0.9375 g
0.3758 g
0.7586 g
0.9000 g
The correct Answer is:A
To solve the problem, we need to determine how much mercury will be left after 260 hours when 1 gram of gold-198 undergoes beta decay.
1. Identify the Half-Life:
The half-life of gold-198 (Au-198) is given as 65 hours.
2. Determine the Total Time:
We need to find out how many half-lives fit into the total time of 260 hours.
Number of half-lives(n)=Total timeHalf-life=260 hours65 hours=4
3. Calculate Remaining Mass of Gold-198:
The remaining mass of the radioactive substance after n half-lives can be calculated using the formula:
Remaining mass=Initial mass×(12)n
Here, the initial mass of Au is 1 gram.
Remaining mass of Au=1 g×(12)4=1 g×116=116 g
4. Calculate the Mass of Mercury Produced:
Since 1 gram of Au-198 decays completely into mercury (Hg), the mass of mercury produced can be calculated as follows:
Mass of Hg produced=Initial mass of Au−Remaining mass of Au
Mass of Hg produced=1 g−116 g=1616 g−116 g=1516 g
5. Convert to Decimal:
To express the mass of mercury in decimal form:
1516 g=0.9375 g
Final Answer:
The amount of mercury produced after 260 hours is 0.9375 grams.
The half-life of gold-198 (Au-198) is given as 65 hours.
We need to find out how many half-lives fit into the total time of 260 hours.
Number of half-lives(n)=Total timeHalf-life=260 hours65 hours=4
The remaining mass of the radioactive substance after n half-lives can be calculated using the formula:
Remaining mass=Initial mass×(12)n
Here, the initial mass of Au is 1 gram.
Remaining mass of Au=1 g×(12)4=1 g×116=116 g
Since 1 gram of Au-198 decays completely into mercury (Hg), the mass of mercury produced can be calculated as follows:
Mass of Hg produced=Initial mass of Au−Remaining mass of Au
Mass of Hg produced=1 g−116 g=1616 g−116 g=1516 g
To express the mass of mercury in decimal form:
1516 g=0.9375 g
The amount of mercury produced after 260 hours is 0.9375 grams.
Similar Questions
1g of .79Au198(t1/2=65hr) decays by β-emission to produce stable Hg.
a. Write nuclear reaction for process.
b. How much Hg will be present after 260 hr.
View SolutionA glass flask of volume 200cm3 is just filled with mercury at 20∘C. The amount of mercury that will overflow when the temperature of the system is raised to 100∘C is (γglass=1.2×10−5/C∘,γmercury=1.8×10−4/C∘)
View Solution
Knowledge Check
Mercury has an angle of contact equal to 140∘ with soda lime galss. A narrow tube of radius 1.00mm made of this glass is dipped in a through containing mercury. By what amount does the mercury dip down in the tube relative to the mercury surface outside? Surface tension of mercury at the temperature of the experiment is 0.465Nm−1. Density of mercury = 13.6×103kgm−3.
A5.34 mmB2.35 mmC6.25 mmD1.44 mm
Calculate the amount of .53I128(t1/2=25min) left after 75 minutes.
View SolutionThe amount of radioactive 52I123(t1/2=25 minutes) left after 50 minutes will be :
View SolutionMercury has an angle of contact of 120∘ with glass. A narrow tube of radius 1.0mm made of the glass is dipped in a through containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside. Surface tension of mercury at the temperature of the experiment os 0.5N/m and density of mercury is 13.6×103kg/m3.
(Take g=9.8m/s2).
View SolutionMercury has an angle of contact equal to 140∘ with soda lime galss. A narrow tube of radius 1.00mm made of this glass is dipped in a through containing mercury. By what amount does the mercury dip down in the tube relative to the mercury surface outside? Surface tension of mercury at the temperature of the experiment is 0.465Nm−1. Density of mercury = 13.6×103kgm−3.
View SolutionThe period of a simple pendulum whose bob is hollow metallic sphere is T. The period is T1 when the bob is filled with sand, T2 where it is filled with mercury and T3 when it is half filled with mercury Which of the following is true?
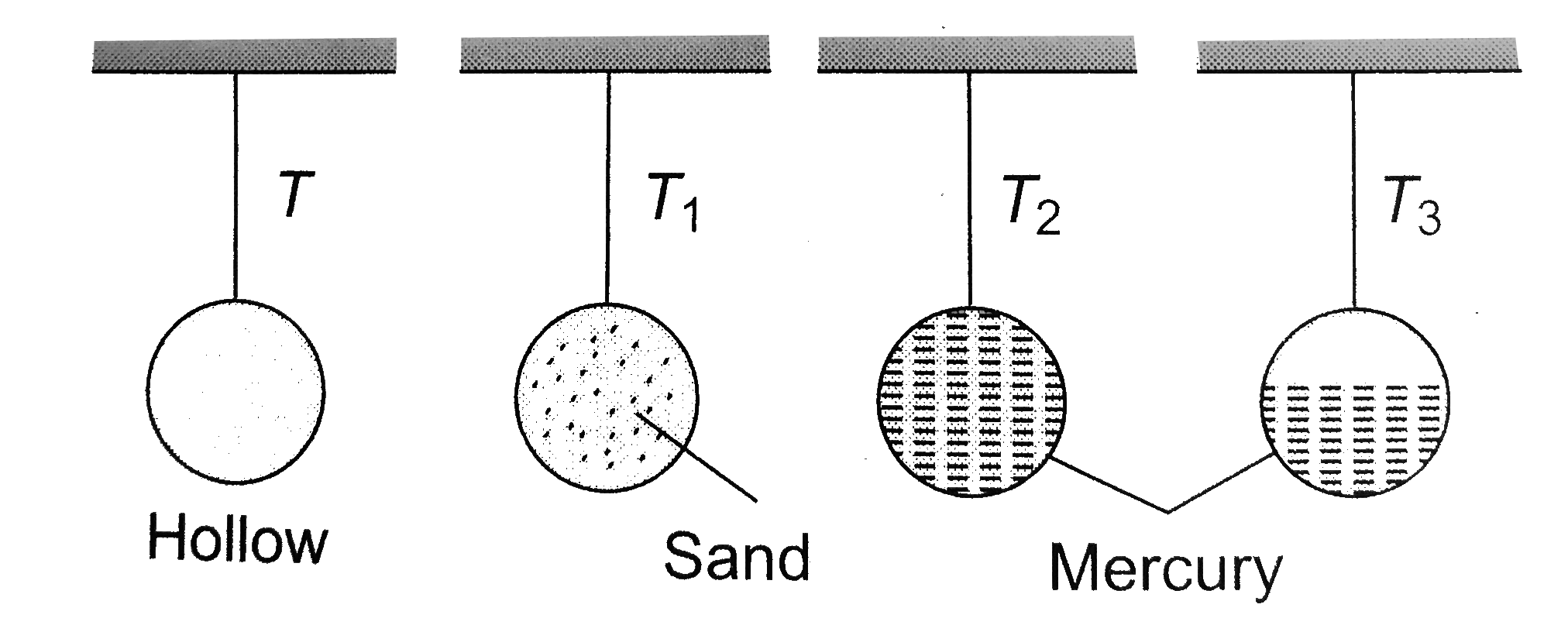
View SolutionA barometer tube is 1 m long and 2cm2 in cross section. Mercury stands to a height of 75cm in the tube. When a small amount of oxygen is introduced in the space above the mercury level, the level falls by 5cm. Calculate the mass of the oxygen is introduced. Room temperature=27∘C, g=10 m s_(-2)anddensityifmercury=13600kg m^(-3).
View SolutionFour vessels A,B,C and D contain respectively 20g atom (T1/2 = 5h) 2g atom (T1/2=1h) 5g atom (T1/2 = 2h) and 10g atom (T1/2 = 3h) of different radio nuclides in the 12 beginning, the maximum activity would be exhibited by the vessel is
View Solution
