The probability that a married man watches a certain T.V. show is 0.6 and the probability that a married woman watches the show is 0.5. The probability that a man watches the show given that his wife does watch is 0.8. If the probability that a wife watches the show given that her husband does watch is k, then 1k is equal to
The correct Answer is:1.5
To solve the problem, we will use the concept of conditional probability. Let's denote the events as follows:
- Let A be the event that a married man watches the show.
- Let B be the event that a married woman watches the show.
Given data:
- P(A)=0.6 (Probability that a married man watches the show)
- P(B)=0.5 (Probability that a married woman watches the show)
- P(A|B)=0.8 (Probability that a man watches the show given that his wife does watch)
We need to find 1k where k=P(B|A) (Probability that a wife watches the show given that her husband does watch).
1. Find P(A∩B):
We can use the formula for conditional probability:
P(A|B)=P(A∩B)P(B)
Rearranging gives:
P(A∩B)=P(A|B)⋅P(B)
Substituting the known values:
P(A∩B)=0.8⋅0.5=0.4
2. Use the formula for P(B|A):
We can again use the conditional probability formula:
P(B|A)=P(A∩B)P(A)
Substituting the values we have:
P(B|A)=P(A∩B)P(A)=0.40.6
3. Calculate P(B|A):
Simplifying the fraction:
P(B|A)=0.40.6=46=23
4. Find k and 1k:
Since k=P(B|A)=23, we need to find 1k:
1k=123=32=1.5
Final Answer:
1k=1.5
- Let B be the event that a married woman watches the show.
- P(A)=0.6 (Probability that a married man watches the show)
- P(B)=0.5 (Probability that a married woman watches the show)
- P(A|B)=0.8 (Probability that a man watches the show given that his wife does watch)
We can use the formula for conditional probability:
P(A|B)=P(A∩B)P(B)
Rearranging gives:
P(A∩B)=P(A|B)⋅P(B)
Substituting the known values:
P(A∩B)=0.8⋅0.5=0.4
We can again use the conditional probability formula:
P(B|A)=P(A∩B)P(A)
Substituting the values we have:
P(B|A)=P(A∩B)P(A)=0.40.6
Simplifying the fraction:
P(B|A)=0.40.6=46=23
Since k=P(B|A)=23, we need to find 1k:
1k=123=32=1.5
1k=1.5
Similar Questions
The probability that a married man watches certain TV show is 0.4 and the probability that a married woman watches the show is 0.5. The probability that a man watches the show, given that his wife does, is 0.7. Then
View SolutionFind the probability that the sum of the numbers showing on two dice is 8, given that at least one die does not show five.
View Solution
Knowledge Check
Craig invited four friends to watch a TV show. He arranged 5 seats in a row. The number of ways he and his four friends can sit in the row is n. In how many of these ways can Craig sit in the middle?
AnBn2Cn3Dn5
Find the probability that the sum of the numbers showing on two dice is 8, given that at least one die does not show five.
View SolutionA bag initially contains 1 red and 2 blue balls. An experiment consisting of selecting a ball at random, noting its color and replacing it together with an additional ball of the same color. If three such trials are made, then (A) Probability that a t least one blue ball is drawn is 0.9 (B) Probability that exactly one blue ball is drawn is 0.2 (C) Probability that all the drawn balls are red given that all the drawn balls are of same color is 0.2 (D) Probability that at least one red bal is drawn is 0.6
View SolutionAn insurance company believes that people can be divided into two classes, those who are accident prone and those who are not. Their statistics show that an accident prone person will not have an accident in a year period with probability 0.4 whereas this probability is 0.2 for the other kind. Given that 30% of people are accident prone, the probability that a new policy holder will have an accident within a year of purchasing a policy is :
View SolutionOne hundred identical coins, each with probability 'p' of showing heads are tossed once. If 0<p<1 and the probability of heads showing on 50 coins is equal to that of heads showing on 51 coins, then the value of p is
View SolutionIn a school, 300 students were surveyed. The survey showed that 186 students liked watching cricket match while the rest disliked it. Out of these students, if one student is chosen at random, what is the probability that the chosen student :
(i) likes watching cricket match?
(ii) dislikes watching cricket match?
View Solution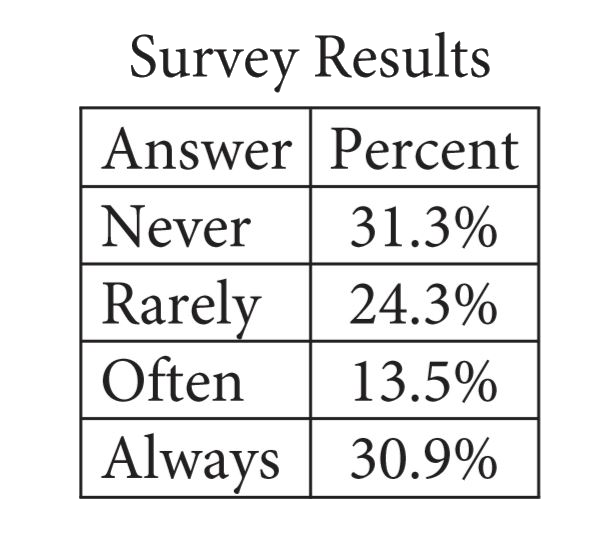
The table above shows the results of a survey in which tablet users were asked how often they would watch video advertisements in order to access streaming content for free. Based on the table, which of the following is closest to the probability that a tablet user answered “Always,” given that the tablet user did not answer “Never”?
View SolutionSuppoe a simple consist of the integers 1,2,….2n, the probability of choosing an integer k is proportion to log k . Show that the conditional probability of choosing the integer 2, given that even integer is chosen is log2(n)log2+log(n!) .
View Solution
