If 11 arithmetic means are inserted between 20 and 10, the number of integral arithmetic means are
1
6
7
8
The correct Answer is:A
To solve the problem of finding the number of integral arithmetic means inserted between 20 and 10, we can follow these steps:
Step 1: Understand the Problem
We need to insert 11 arithmetic means between the numbers 20 and 10. This means we will have a total of 13 terms in an arithmetic progression (AP): the first term (a1) is 20, the last term (a13) is 10, and the 11 terms in between are a2, a3, ..., a12.
Step 2: Use the Formula for the nth Term of an AP
The nth term of an arithmetic progression can be expressed as:
an=a+(n−1)d
where a is the first term, d is the common difference, and n is the term number.
Step 3: Set Up the Equation
For our case:
- a1=20
- a13=10
- We need to find d.
Using the formula for the 13th term:
a13=a1+(13−1)d
Substituting the known values:
10=20+12d
Step 4: Solve for d
Rearranging the equation gives:
10−20=12d
−10=12d
d=−1012=−56
Step 5: Write the General Term
Now, we can express the general term an:
an=20+(n−1)(−56)
an=20−5(n−1)6
Step 6: Find Integral Values
For an to be an integer, the term −5(n−1)6 must also be an integer. This means that n−1 must be a multiple of 6.
Let:
n−1=6k
Then:
n=6k+1
Step 7: Determine k Values
Since we need n to be between 2 and 12 (inclusive) to ensure we have 11 arithmetic means:
- For k=0: n=1 (not valid, as it corresponds to the first term)
- For k=1: n=7 (valid)
- For k=2: n=13 (not valid, exceeds the number of means)
Conclusion
The only valid value for k is 1, which gives us n=7. This means there is only 1 integral arithmetic mean that can be inserted between 20 and 10.
We need to insert 11 arithmetic means between the numbers 20 and 10. This means we will have a total of 13 terms in an arithmetic progression (AP): the first term (a1) is 20, the last term (a13) is 10, and the 11 terms in between are a2, a3, ..., a12.
The nth term of an arithmetic progression can be expressed as:
an=a+(n−1)d
where a is the first term, d is the common difference, and n is the term number.
For our case:
- a1=20
- a13=10
- We need to find d.
a13=a1+(13−1)d
Substituting the known values:
10=20+12d
Rearranging the equation gives:
10−20=12d
−10=12d
d=−1012=−56
Now, we can express the general term an:
an=20+(n−1)(−56)
an=20−5(n−1)6
For an to be an integer, the term −5(n−1)6 must also be an integer. This means that n−1 must be a multiple of 6.
n−1=6k
Then:
n=6k+1
Since we need n to be between 2 and 12 (inclusive) to ensure we have 11 arithmetic means:
- For k=0: n=1 (not valid, as it corresponds to the first term)
- For k=1: n=7 (valid)
- For k=2: n=13 (not valid, exceeds the number of means)
The only valid value for k is 1, which gives us n=7. This means there is only 1 integral arithmetic mean that can be inserted between 20 and 10.
Similar Questions
Find the arithmetic mean of:
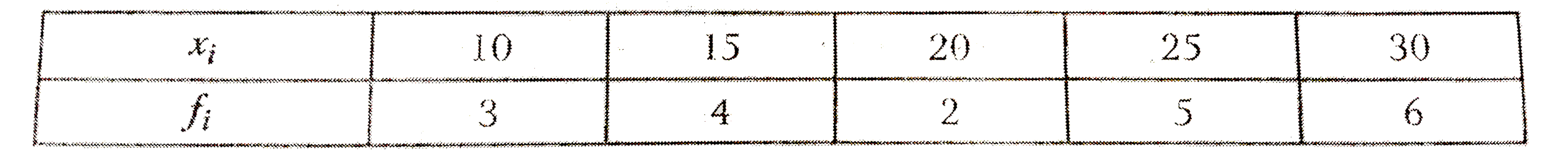
View SolutionIf n arithmetic means are inserted between 2 and 38, then the sum of the resulting series is obtained as 200. Then find the value of n.
View SolutionIf n arithmetic means are inserted between 2 and 38, then the sum of the resulting series is obtained as 200. Then find the value of n.
View SolutionIf p arithmetic means are inserted between a and b, prove that d=b−ap+1
View SolutionIf n arithmetic means are inserted between 1 and 31 such that the ratio of the first mean and nth mean is 3:29 then the value of n is
a.10 b. 12 c. 13 d. 14
View SolutionIf G1 and G2 are two geometric means inserted between any two numbers and A is the arithmetic mean of two numbers, then the value of G21G2+G22G1 is:
View SolutionInsert five arithmetic means between 20 and 32 .
View SolutionInsert 3 arithmetic means between 2 and 10.
View SolutionSuppose that n arithmetic means are inserted between then numbers 7 and 49. If the sum of these means is 364 then the sum their squares is
View SolutionIf n arithmetic means are inserted between 7 and 71 such that 5th A.M. is 27 then n=?
View Solution
