In a nuclear reactor, the fuel is consumed at the rate of 1mg/s. The power generated in kilowatt is.
9×104
9×107
9×108
9×1012
The correct Answer is:B
To solve the problem of calculating the power generated in a nuclear reactor where the fuel is consumed at a rate of 1 mg/s, we can follow these steps:
1. Understand the Given Data:
- The rate of fuel consumption is given as mt=1mg/s.
- We need to convert this rate into kilograms for standard SI units.
- 1mg=1×10−6kg.
2. Convert the Fuel Consumption Rate:
- Convert 1 mg/s to kg/s:
mt=1mg/s=1×10−6kg/s
3. Use the Energy-Mass Equivalence:
- According to Einstein's equation, the energy E produced from mass m is given by:
E=mc2
- Here, c (the speed of light) is approximately 3×108m/s.
4. Calculate the Energy Produced Per Second:
- Since we are looking for power, which is energy per unit time, we can express power P as:
P=Et=mc2t
- Since mt=1×10−6kg/s, we can substitute this into the equation:
P=(1×10−6kg/s)⋅(3×108m/s)2
5. Calculate c2:
- Calculate c2:
c2=(3×108)2=9×1016m2/s2
6. Substitute and Calculate Power:
- Now substitute c2 back into the power equation:
P=1×10−6⋅9×1016=9×1010W
7. Convert Watts to Kilowatts:
- Since 1kW=1000W, convert power to kilowatts:
P=9×10101000=9×107kW
8. Final Answer:
- The power generated in the nuclear reactor is:
P=9×107kW
- The rate of fuel consumption is given as mt=1mg/s.
- We need to convert this rate into kilograms for standard SI units.
- 1mg=1×10−6kg.
- Convert 1 mg/s to kg/s:
mt=1mg/s=1×10−6kg/s
- According to Einstein's equation, the energy E produced from mass m is given by:
E=mc2
- Here, c (the speed of light) is approximately 3×108m/s.
- Since we are looking for power, which is energy per unit time, we can express power P as:
P=Et=mc2t
- Since mt=1×10−6kg/s, we can substitute this into the equation:
P=(1×10−6kg/s)⋅(3×108m/s)2
- Calculate c2:
c2=(3×108)2=9×1016m2/s2
- Now substitute c2 back into the power equation:
P=1×10−6⋅9×1016=9×1010W
- Since 1kW=1000W, convert power to kilowatts:
P=9×10101000=9×107kW
- The power generated in the nuclear reactor is:
P=9×107kW
Similar Questions
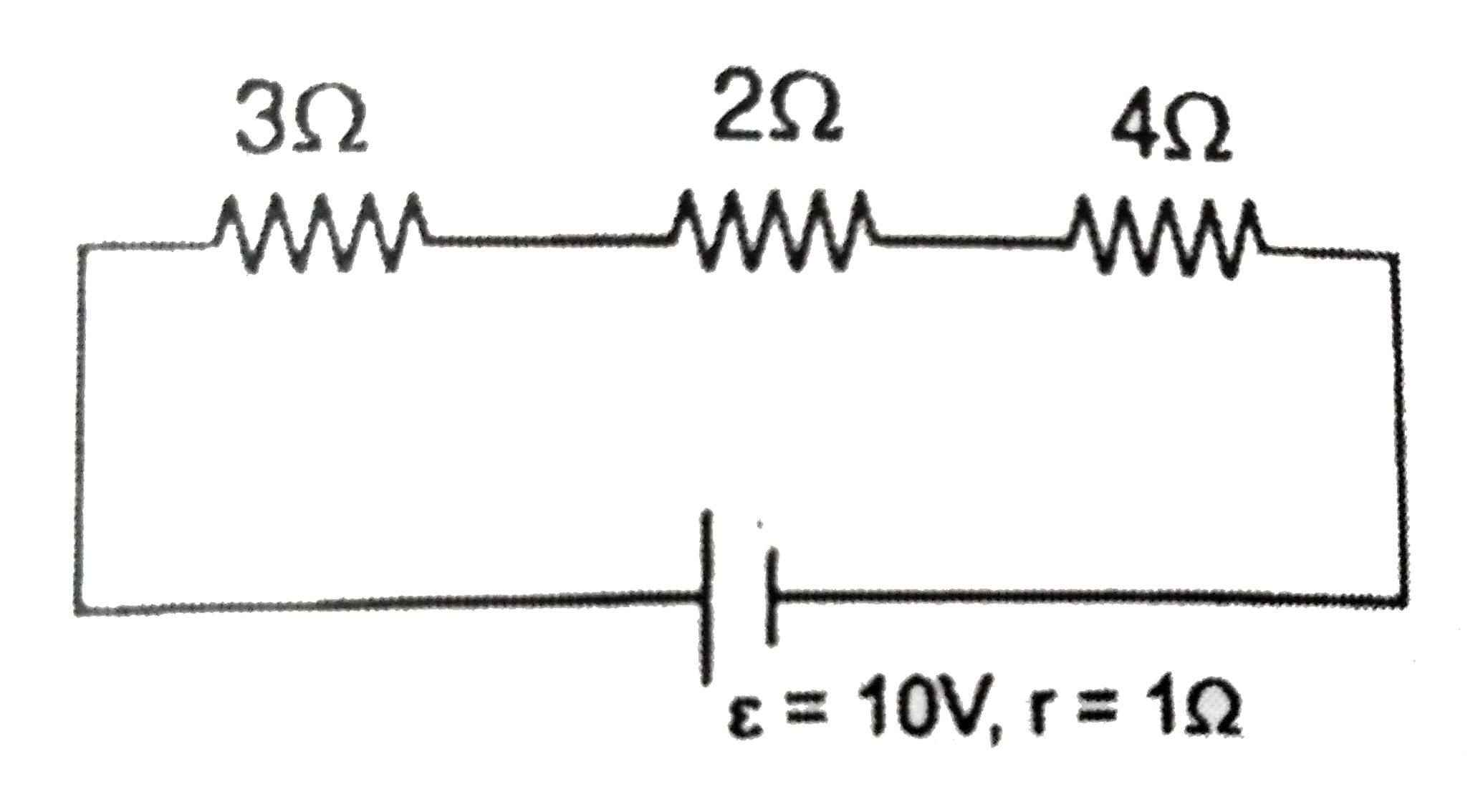
In given circuit determine
(a) Equivalent resistance (Including internal resistance).
(b) Current I,i1,i2' and i3
( c) Potential difference across battery and each resistance
(d) The rate at which the chemical energy of the cell is consumed
(e ) The rate at which heat is generated insisde the battry
(f) Electric power output
(g) Which resistance consumes miximum power ?
(h) Power dissipated across 4Ω resistance.

View SolutionIn the given circuit determine
(a) Equivalent resistance (Including internal resistance ).
(b) Current in each resistance
( c) Potential difference across each resistance
(d) The rate awich the chemical energy of the cell is consumed
( e) The rate at which heat is generated inside the battery
(f) Electric power output
(h) Which resistance consumes maximum power
(f) Power dissipated in 3Ω resistance.
View SolutionThe mass defect in a particular nuclear reaction is 0.3 grams. The amont of energy liberated in kilowatt hours is.
(Velocity of light =3×108m/s).
View SolutionThe mass defect in a particular nuclear reaction is 0.3 grams. The amont of energy liberated in kilowatt hours is.
(Velocity of light =3×108m/s).
View SolutionIn a rocket, fuel bums at the rate of 1 kg/s. This fuel is ejected from the rocket with a velocity of 60 km/s. This exerts a force on the rocket equal to
View SolutionIn a rocket, fuel burns at the rate of 2 kg/s. This fuel gets ejected from the rocket with a velocity of 80 km/s. Force exerted on the rocket is -
View SolutionIn a rocket, fuel burns at the rate of 2 kg/s. This fuel gets ejected from the rocket with a velocity of 80 km/s. Force exerted on the rocket is -
View SolutionIn a certain nuclear reactor, a radioactive nucleus is bieng produced at a constant rate =1000/s The mean life of the radionuclide is 40 minutes. At steady state, the number of radionuclide will be
View SolutionIn a nuclear reactor ^235U undergoes fission liberating 200 MeV of energy. The reactor has a 10% efficiency and produces 1000 MW power. If the reactor is to function for 10 yr, find the total mass of uranium required.
View SolutionA bus diver drove at an average speed of 45 miles per hour for 3 hours while the bus consumed fuel at a rate of 15 miles per gallon. How many gallons of fuel did the bus use for the entire 3 - hour trip?
View Solution
