A galvanometer of resistance measures . shunt required to increase range up tow 2 A is
The correct Answer is:A
To solve the problem of finding the shunt resistance required to increase the range of a galvanometer, we can follow these steps:
1. Identify the Given Values:
- Resistance of the galvanometer, G=25Ω
- Current through the galvanometer, Ig=10−3A
- Total current for the new range, I=2A
2. Understand the Circuit Configuration:
- The galvanometer is connected in parallel with a shunt resistor S.
- The current through the galvanometer is Ig and the current through the shunt is I−Ig.
3. Apply the Voltage Equality in Parallel:
- Since the galvanometer and shunt are in parallel, the voltage across both must be the same:
Ig⋅G=(I−Ig)⋅S
4. Substitute the Known Values:
- Substitute Ig=10−3A, G=25Ω, and I=2A:
10−3⋅25=(2−10−3)⋅S
5. Simplify the Equation:
- Calculate the left side:
25⋅10−3=0.025
- The right side becomes:
(2−0.001)⋅S=1.999⋅S
- Therefore, we have:
0.025=1.999⋅S
6. Solve for the Shunt Resistance S:
- Rearranging gives:
S=0.0251.999
- Approximating 1.999 as 2:
S≈0.0252=0.0125Ω
7. Convert to Milliohms:
- Since 0.0125Ω=12.5mΩ.
Final Answer:
The shunt resistance required to increase the range up to 2 A is approximately 12.5mΩ.
- Resistance of the galvanometer, G=25Ω
- Current through the galvanometer, Ig=10−3A
- Total current for the new range, I=2A
- The galvanometer is connected in parallel with a shunt resistor S.
- The current through the galvanometer is Ig and the current through the shunt is I−Ig.
- Since the galvanometer and shunt are in parallel, the voltage across both must be the same:
Ig⋅G=(I−Ig)⋅S
- Substitute Ig=10−3A, G=25Ω, and I=2A:
10−3⋅25=(2−10−3)⋅S
- Calculate the left side:
25⋅10−3=0.025
- The right side becomes:
(2−0.001)⋅S=1.999⋅S
- Therefore, we have:
0.025=1.999⋅S
- Rearranging gives:
S=0.0251.999
- Approximating 1.999 as 2:
S≈0.0252=0.0125Ω
- Since 0.0125Ω=12.5mΩ.
The shunt resistance required to increase the range up to 2 A is approximately 12.5mΩ.
Similar Questions
A galvanometer of resistance 22.8Ω measures 1 A. How much shunt should be used , so that it can be used to measure 20 A ?
View SolutionA galvanometer of resistance 40Ω can measure a current of 10mA To convert it into a voltmeter of range 8V the required resistance is ___________ Ω.
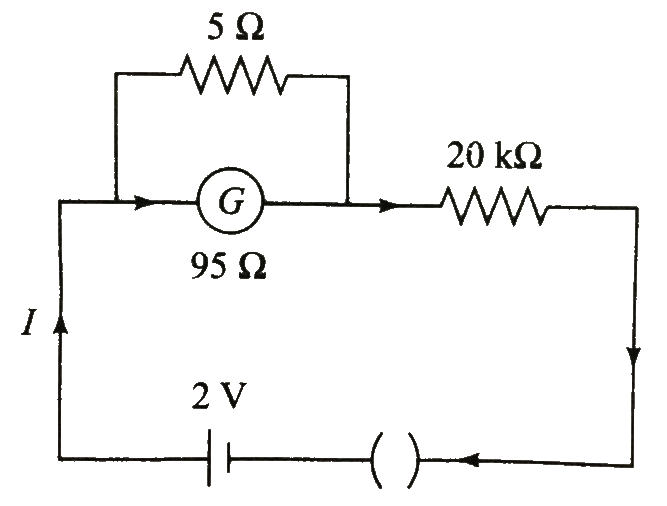
View SolutionA galvanometer of resistance 95Ω, shunted resistance of 5Ω, gives a deflection of 50 divisions when joined in series with a resistance of 20kΩ and a 2V accumulator. What is the current sensitivity of the galvanomter (in div/μA)?
View SolutionA galvanometer of resistance 100Ω gives full deffection for a current 10−5 the value of shunt required to convert it into ammeter of range 1 ampere is:-
View SolutionA galvanometer has a resistance of 100Ω. A current of 10−3A pass through the galvanometer. How can it be converted into (a) ammeter of range 10 A and (b) voltmeter of range 10v.
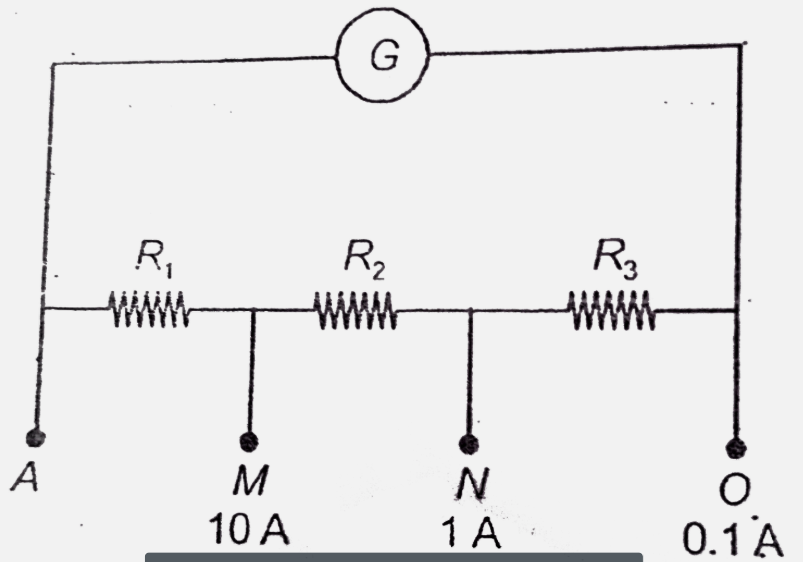
View SolutionThe galvanometer shown in figure has resistance 50 Ω and current required for full scale deflection is 1mA. Find the resistance R1,R2 and required to convert to convert it into ammeter having ranges as indicated.
View SolutionA voltmeter has resistance 2000Ω and range 5 V. For increasing its range upto 20V, a resistance of
View SolutionA galvanometer of resistance 20Ω is shunted by a 2Ω resistor. What part of the main current flows through the galvanometer ?
View SolutionAn ammeter of resistance 0.6Ω can measure current upto 1.0 A. Calculate (i) The shunt resistance required to enable the ammeter to measure current upto 5.0 A (ii) The combined resistance of the ammeter and the shunt.
View SolutionA galvanometer of resistance 25Ω gives full scale deflection for a current of 10 milliampere , is to be changed into a voltmeter of range 100 V by connecting a resistance of ‘ R ’ in series with galvanometer. The value of resistance R in Ω is
View Solution
