The maximum transverse velocity and maximum transverse acceleration of a harmonic wave in a one - dimensional string are 1ms−1and1ms−2 respectively. The phase velocity of the wave is 1ms−1. The waveform is
sin(x−t)
sin(x−2t)
sin(x2−t)
sin(x−t2)
The correct Answer is:A
To solve the problem, we need to derive the wave equation based on the given parameters: maximum transverse velocity, maximum transverse acceleration, and phase velocity. Let's break it down step by step.
Step 1: Understand the given parameters
We have:
- Maximum transverse velocity, Vmax=1ms−1
- Maximum transverse acceleration, Amax=1ms−2
- Phase velocity, v=1ms−1
Step 2: Use the formulas for maximum velocity and acceleration
In simple harmonic motion (SHM), the maximum transverse velocity and maximum transverse acceleration are given by:
- Vmax=Aω
- Amax=Aω2
Where:
- A is the amplitude
- ω is the angular frequency
Step 3: Set up the equations
From the maximum velocity:
1=Aω(1)
From the maximum acceleration:
1=Aω2(2)
Step 4: Solve for A and ω
From equation (1), we can express A in terms of ω:
A=1ω(3)
Substituting equation (3) into equation (2):
1=(1ω)ω2
This simplifies to:
1=ω2ω⟹1=ω
Thus, we find:
ω=1rad/s
Step 5: Find the amplitude A
Substituting ω=1 back into equation (3):
A=11=1m
Step 6: Calculate the wave number k
The phase velocity v is related to ω and k by the equation:
v=ωk
Rearranging gives:
k=ωv
Substituting ω=1 and v=1:
k=11=1m−1
Step 7: Write the wave equation
The general form of the wave equation is:
y=Asin(kx−ωt)
Substituting A=1, k=1, and ω=1:
y=1sin(1x−1t)=sin(x−t)
Final Answer
The waveform is:
y=sin(x−t)
We have:
- Maximum transverse velocity, Vmax=1ms−1
- Maximum transverse acceleration, Amax=1ms−2
- Phase velocity, v=1ms−1
In simple harmonic motion (SHM), the maximum transverse velocity and maximum transverse acceleration are given by:
- Vmax=Aω
- Amax=Aω2
- A is the amplitude
- ω is the angular frequency
From the maximum velocity:
1=Aω(1)
From the maximum acceleration:
1=Aω2(2)
From equation (1), we can express A in terms of ω:
A=1ω(3)
1=(1ω)ω2
This simplifies to:
1=ω2ω⟹1=ω
Thus, we find:
ω=1rad/s
Substituting ω=1 back into equation (3):
A=11=1m
The phase velocity v is related to ω and k by the equation:
v=ωk
Rearranging gives:
k=ωv
Substituting ω=1 and v=1:
k=11=1m−1
The general form of the wave equation is:
y=Asin(kx−ωt)
Substituting A=1, k=1, and ω=1:
y=1sin(1x−1t)=sin(x−t)
The waveform is:
y=sin(x−t)
Similar Questions
A harmonically moving transverse wave on a string has a maximum particle velocity and acceleration of 3 m/s and 90m/s2 respectively. Velocity of the wave is 20m/s. Find the waveform.
View SolutionA transverse mechanical harmonic wave is travellling on a string. Maximum velocity and maximum acceleration of a particle on the string are 3m/s and 90m/s2, respectively. If the wave is travelling with a speed of 20m/s on the string, write wave function describing the wave. \
View SolutionA car is travelling on a straight road. The maximum velocity the car Can attain is 24ms−1. The maximum acceleration and deceleration it can attain are 1ms−2 and 4ms−2 respectively. The shortest time the car takes from rest to rest in a distance of 200 m is,
View SolutionVelocity and acceleration of a particle at some instant of time are v=(3ˆi+4ˆj)ms−1 and a=−(6ˆi+8ˆj)ms−2 respectively. At the same instant particle is at origin. Maximum x-coordinate of particle will be
View SolutionFind the velocity of image,when object and mirror both are moving towards each other with velocities 4ms−1and5ms−1 respectively, is
View SolutionThe minimum and maximum velocities of a projectile are 10ms−1 and 20ms−1 respectively. The horizontal range and maximum height are respectively (g=10 ms−2)
View SolutionA transverse wave travelling in a string produce maximum transverse velocity of 3m/s and maximum transverse acceleration 90m/s2 in a particle. If the velocity of wave in the string is 20m/s. Datermine the equation of the wave ?
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
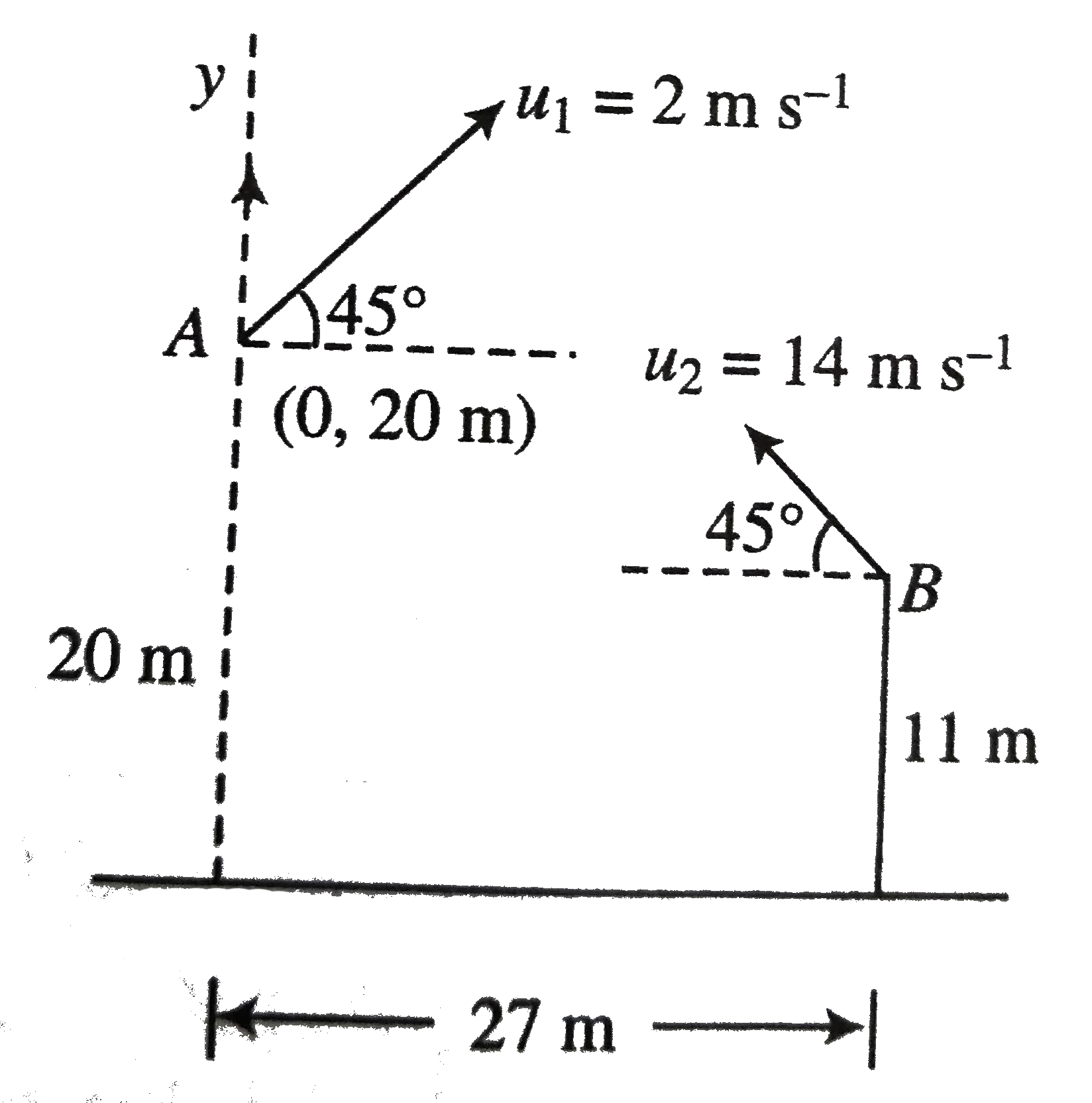
The relative velocity of B as seen from A in
View SolutionThe maximum range of a gun on horizontal terrain is 1km. If g=10ms−2, what must be the muzzle velocity of the shell ?
View SolutionThe wavelength of the radiowaves transmitted by a broadcasting station is 422.54m. What is the frequency of the wave? Velocity of the wave =3×108ms−1.
View Solution
