Two particles P and Q are moving on circle. At a certain instant of time both the particles and diametrically opposite and P has tangential acceleration 8m/s2 and centripetal acceleration 5m/s2 whereas Q has only e centripetal acceleration of1m/s2. At that instant acceleration (inm/s2) of P with respect to Q is
14
√80
10
12
The correct Answer is:C
To find the acceleration of particle P with respect to particle Q, we will follow these steps:
Step 1: Identify the accelerations of both particles
- Particle P has:
- Tangential acceleration, atP=8m/s2
- Centripetal acceleration, acP=5m/s2
- Particle Q has:
- Centripetal acceleration, acQ=1m/s2
- (No tangential acceleration)
Step 2: Represent the accelerations as vectors
- Since P and Q are diametrically opposite, we can represent their accelerations in a coordinate system.
- Let's assume:
- The tangential acceleration of P acts in the positive y-direction.
- The centripetal acceleration of P acts in the negative x-direction.
- The centripetal acceleration of Q acts in the positive x-direction.
Thus, we can write:
- Acceleration of P, →aP=(−5^i+8^j)m/s2
- Acceleration of Q, →aQ=(1^i)m/s2
Step 3: Calculate the relative acceleration of P with respect to Q
The relative acceleration of P with respect to Q is given by:
→aPQ=→aP−→aQ
Substituting the values:
→aPQ=(−5^i+8^j)−(1^i)=(−5−1)^i+8^j=(−6^i+8^j)m/s2
Step 4: Calculate the magnitude of the relative acceleration
To find the magnitude of →aPQ, we use the Pythagorean theorem:
|→aPQ|=√(−6)2+(8)2=√36+64=√100=10m/s2
Final Answer
The acceleration of P with respect to Q is 10m/s2.
---
- Particle P has:
- Tangential acceleration, atP=8m/s2
- Centripetal acceleration, acP=5m/s2
- Centripetal acceleration, acQ=1m/s2
- (No tangential acceleration)
- Since P and Q are diametrically opposite, we can represent their accelerations in a coordinate system.
- Let's assume:
- The tangential acceleration of P acts in the positive y-direction.
- The centripetal acceleration of P acts in the negative x-direction.
- The centripetal acceleration of Q acts in the positive x-direction.
- Acceleration of P, →aP=(−5^i+8^j)m/s2
- Acceleration of Q, →aQ=(1^i)m/s2
The relative acceleration of P with respect to Q is given by:
→aPQ=→aP−→aQ
Substituting the values:
→aPQ=(−5^i+8^j)−(1^i)=(−5−1)^i+8^j=(−6^i+8^j)m/s2
To find the magnitude of →aPQ, we use the Pythagorean theorem:
|→aPQ|=√(−6)2+(8)2=√36+64=√100=10m/s2
The acceleration of P with respect to Q is 10m/s2.
Similar Questions
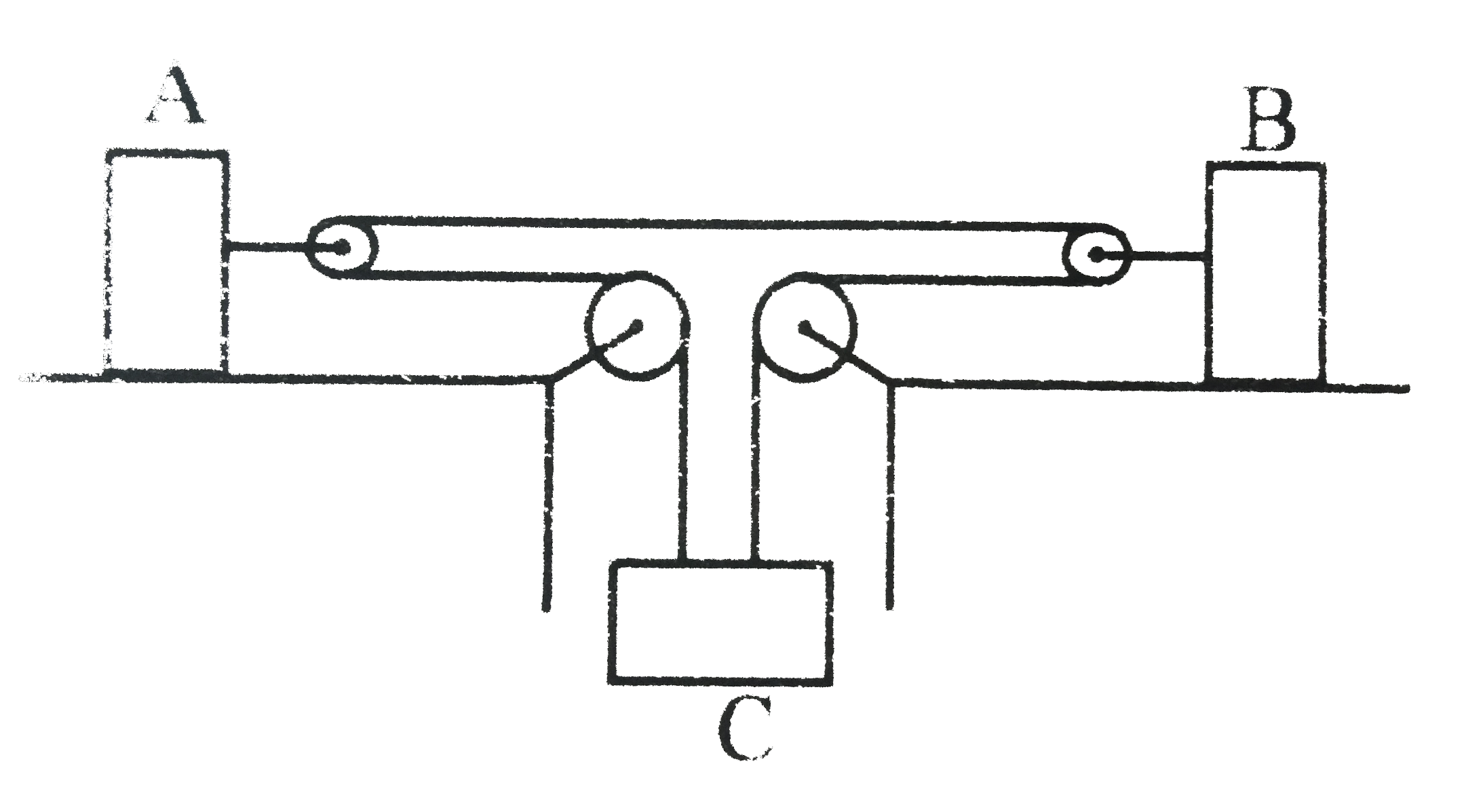
If acceleration of A is 2m/s2 to left and acceleration of B is 1m/s2 to left, then acceleration of C is-
View SolutionCar A has an acceleration of 2m/s2 due east and car B,4m/s2. due north. What is the acceleration of car B with respect to car A?
View SolutionCar A has an acceleration of 2m/s2 due east and car B,4m/s2. due north. What is the acceleration of car B with respect to car A?
View SolutionA particle starts moving with acceleration 2m/s2. Distance travelled by it in 5th half second is
View SolutionFigur shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5m at a given instant of time. At this instant, find:
(a) the radius acceleration,
(b) the speed of the acceleration,
(c) its tangential acceleration.

View SolutionA particle is moving with a constant angular acceleration of 4rad/s2 in a circular path. At time t=0 , particle was at rest. Find the time at which the magnitudes of centripetal acceleration and tangential acceleration are equal.
View SolutionA particle moves in a circle with constant tangential acceleration starting from rest. At t = 1/2 s radial acceleration has a value 25% of tangential acceleration. The value of tangential acceleration will be correctly represented by
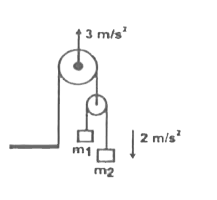
View SolutionIn the figure shown, the acceleration of block of mass m2 is 2m/s2. The acceleration of m1 :
View SolutionA particle has an initial velocity of 9m/s due east and a constant acceleration of 2m/s2 due west. The distance coverd by the particle in the fifth second of its motion is :
View SolutionA particle is moving on a circular path of radius 1 m with 2 m/s. If speed starts increasing at a rate of 2m/s2, then acceleration of particle is
View Solution
