Find the magnitude of the magnetic field at the center of an equilateral triangular loop of side length 1m which is carrying a current of 10A. ( Take μ0=4π×10−7NA−2)
3μT
1μT
18μT
9μT
The correct Answer is:C
To find the magnitude of the magnetic field at the center of an equilateral triangular loop carrying a current, we can follow these steps:
Step 1: Understand the Geometry of the Triangle
An equilateral triangle has all sides equal. Given that the side length is 1 meter, we can denote the vertices of the triangle as A, B, and C.
Step 2: Determine the Perpendicular Distance (r) from the Center to a Side
The perpendicular distance from the center of the triangle to any side can be calculated using the formula for the height (h) of an equilateral triangle:
h=√32×side length
For our triangle:
h=√32×1=√32 meters
The distance from the center to the side (r) is:
r=h3=√3/23=√36 meters
Step 3: Calculate the Magnetic Field Due to One Side
The magnetic field (B) at the center due to one side of the triangle is given by the formula:
Bone side=μ0I4πrsin(60∘)
Where:
- μ0=4π×10−7N/A2
- I=10A
- sin(60∘)=√32
Substituting the values:
Bone side=(4π×10−7)×104π×√36⋅√32
This simplifies to:
Bone side=10×6√3×10−7 T
Step 4: Total Magnetic Field at the Center
Since there are three sides contributing to the magnetic field at the center, we multiply the magnetic field due to one side by 3:
Btotal=3×Bone side
Substituting the expression from above:
Btotal=3×10×6√3×10−7 T
This simplifies to:
Btotal=180√3×10−7 T
Step 5: Final Calculation
Calculating the numerical value:
Btotal=60√3×10−7 T
Using √3≈1.732:
Btotal≈60×1.732×10−7≈1.0392×10−5 T≈10.39μT
Conclusion
The magnitude of the magnetic field at the center of the equilateral triangular loop is approximately:
B≈10.39μT
An equilateral triangle has all sides equal. Given that the side length is 1 meter, we can denote the vertices of the triangle as A, B, and C.
The perpendicular distance from the center of the triangle to any side can be calculated using the formula for the height (h) of an equilateral triangle:
h=√32×side length
For our triangle:
h=√32×1=√32 meters
The distance from the center to the side (r) is:
r=h3=√3/23=√36 meters
The magnetic field (B) at the center due to one side of the triangle is given by the formula:
Bone side=μ0I4πrsin(60∘)
Where:
- μ0=4π×10−7N/A2
- I=10A
- sin(60∘)=√32
Bone side=(4π×10−7)×104π×√36⋅√32
This simplifies to:
Bone side=10×6√3×10−7 T
Since there are three sides contributing to the magnetic field at the center, we multiply the magnetic field due to one side by 3:
Btotal=3×Bone side
Substituting the expression from above:
Btotal=3×10×6√3×10−7 T
This simplifies to:
Btotal=180√3×10−7 T
Calculating the numerical value:
Btotal=60√3×10−7 T
Using √3≈1.732:
Btotal≈60×1.732×10−7≈1.0392×10−5 T≈10.39μT
The magnitude of the magnetic field at the center of the equilateral triangular loop is approximately:
B≈10.39μT
Similar Questions
Find the magnitude of the magnetic fieldat the center of an equilateral triangular loop of side length 1m which is carrying a current of 10A. ( Take μ0=4π×10−7NA−2)
View SolutionThe magnitude of the magnetic field at the center of an equilateral triangular loop of side 1 m which is carrying a current of 10 A (in μT) is ___________ .
[Take μ0=4π×10−7NA−2]
View SolutionThe magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
View SolutionFind the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
View SolutionFind the magnetic field at point P due to a straight line segment AB of length 6cm carrying a current of 5A. (See figure)
(μ0=4π×10−7N−A−2).
 .
.
View SolutionMagnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
View SolutionA long straight wire is carrying a current of 12 A . The magnetic field at a distance of 8 cm is
(μ0=4π×10−7NA2)
View SolutionMagnitude of magnetic field (in SI units) at the centre of a hexagonal shape coil of side 10cm , 50 turns and carrying current I (Ampere) in units of μ0Iπ is :
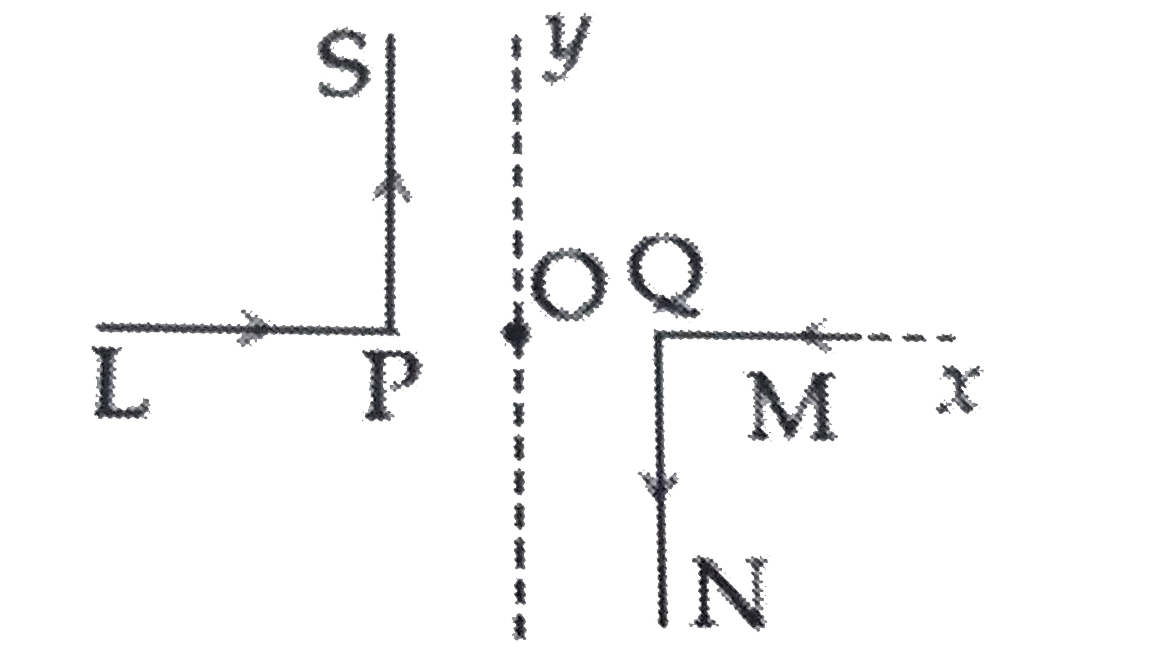
View SolutionAs shown in the figure two infinitely long, identical wires are bent by 90∘ and placed in such a way that the segments LP and QM are along the x-axis , while segments PS and QN are parallel to the Y-axis If OP=OQ=4 cm ,and the magnitude of the magnetic field at O is 10−4 T, and the magnitude of the current in each wire and the direction of the magnetic field at O will be
(μo=4π×10−7NA−2):
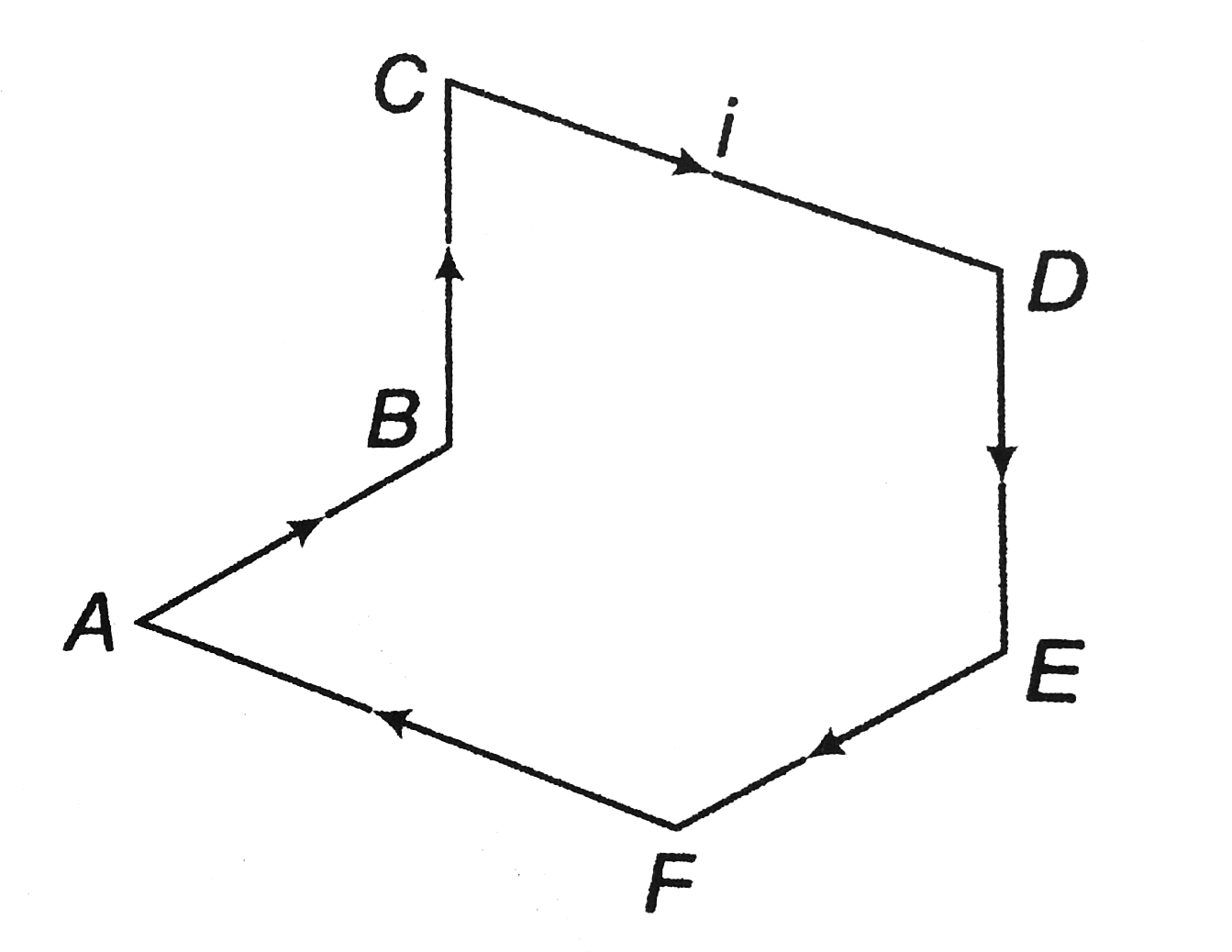
View SolutionFind the magnitude of magetic moment of the current carrying lop ABCDEFA. Each side of the loop is 10cm long and current in the loop is i=2.0A
View Solution
