For the reaction : aA→bB, it is given that
log[−dAdt]=log[dBdt]+0.6020. What is a:b is ?
4
2
1.5
0
The correct Answer is:A
To solve the problem, we need to analyze the given equation and derive the stoichiometric ratio a:b for the reaction aA→bB.
1. Understanding the Rate of Reaction:
The rate of disappearance of A is given as:
−d(A)dt=k(A)a
The rate of appearance of B is given as:
d(B)dt=k(B)b
2. Using the Given Equation:
We are given:
log(−dAdt)=log(dBdt)+0.6020
This can be rewritten using properties of logarithms:
log(−dAdt)−log(dBdt)=0.6020
Which simplifies to:
log(−dA/dtdB/dt)=0.6020
3. Exponentiating Both Sides:
By exponentiating both sides, we can eliminate the logarithm:
−dA/dtdB/dt=100.6020
We know that 100.6020 is approximately equal to 4 (since 100.6020≈4).
4. Setting Up the Ratio:
Therefore, we have:
−dA/dtdB/dt=4
This implies:
−dA=4dB
Hence, we can express this in terms of stoichiometric coefficients:
dAdB=14
5. Finding the Stoichiometric Ratio:
From the above relationship, we can conclude that:
a:b=4:1
Final Answer:
Thus, the ratio a:b is 4:1.
The rate of disappearance of A is given as:
−d(A)dt=k(A)a
The rate of appearance of B is given as:
d(B)dt=k(B)b
We are given:
log(−dAdt)=log(dBdt)+0.6020
This can be rewritten using properties of logarithms:
log(−dAdt)−log(dBdt)=0.6020
Which simplifies to:
log(−dA/dtdB/dt)=0.6020
By exponentiating both sides, we can eliminate the logarithm:
−dA/dtdB/dt=100.6020
We know that 100.6020 is approximately equal to 4 (since 100.6020≈4).
Therefore, we have:
−dA/dtdB/dt=4
This implies:
−dA=4dB
Hence, we can express this in terms of stoichiometric coefficients:
dAdB=14
From the above relationship, we can conclude that:
a:b=4:1
Thus, the ratio a:b is 4:1.
Similar Questions
For the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
In the following reaction,
xA→yB
log.[−d[A]dt]=log.[d[B]dt]+0.3
where negative isgn indicates rate of disappearance of the reactant. Thus, x:y is:
View SolutionMechanism of the reaction is:
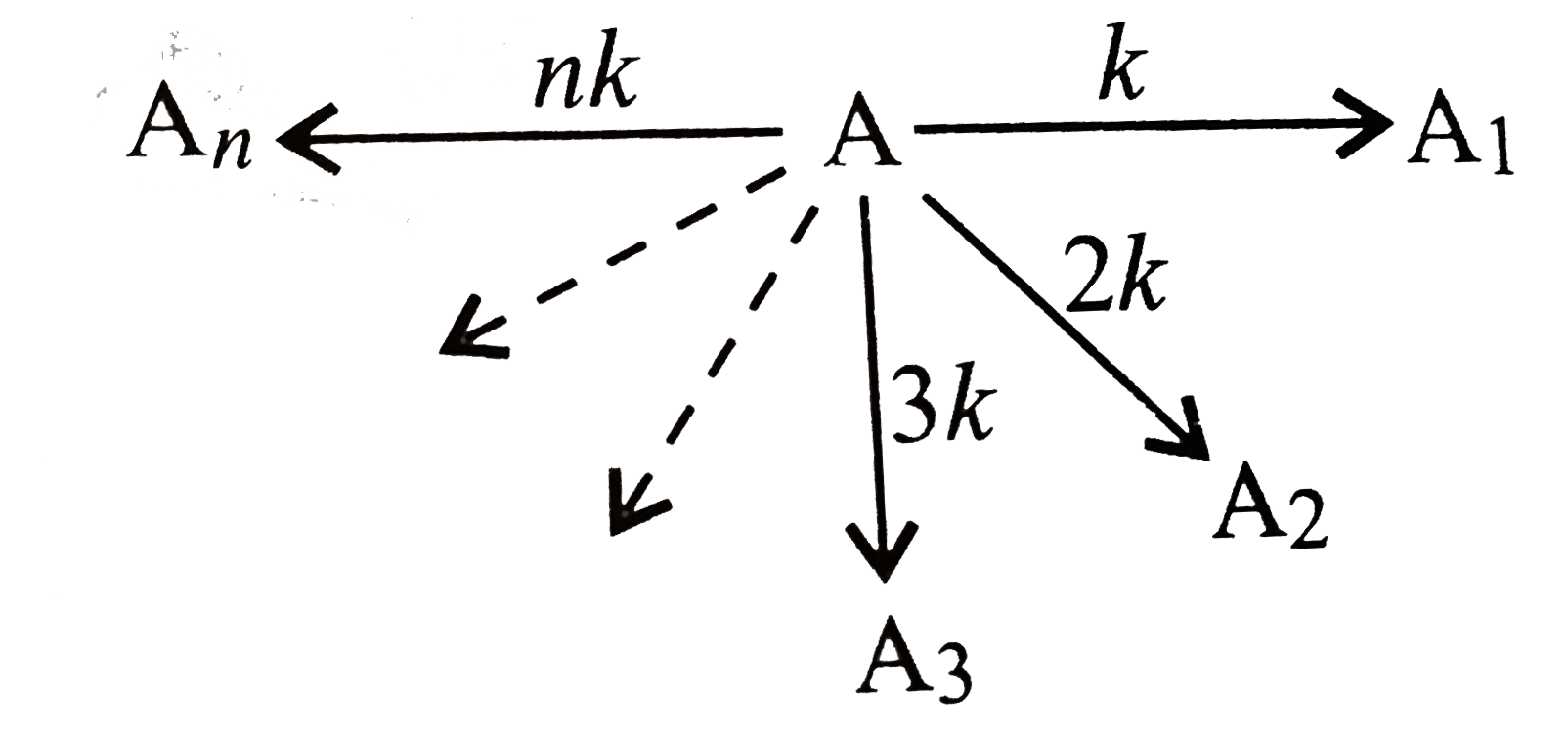
What is (a) −d[A]dt, (b) d[A1]dt
View Solution
Knowledge Check
At any stage of the reaction 3A →2B, the reaction rate +dBdt will be equal to
A−3dAdtB−dAdtC−23dAdtD−32dAdtAt any stage of the reaction 3A →2B, the reaction rate +dBdt will be equal to
A−3dAdtB−dAdtC−23dAdtD−32dAdtAt any stage of the reaction 3A →2B, the reaction rate +dBdt will be equal to
A−3dAdtB−dAdtC−23dAdtD−32dAdt
For a reaction B+2D→3T, it is given that −dCadt=kCaC2D. The expression for −dCDdt will be:
View SolutionFor a reaction A→ B, the rate of reaction can be denoted by −dAdtordBdtState the significance of plus and minus signs in this case.
View SolutionFor a reaction A→ B, the rate of reaction can be denoted by −dAdtordBdtState the significance of plus and minus signs in this case.
View SolutionFor a reaction A→ B, the rate of reaction can be denoted by −dAdtordBdtState the significance of plus and minus signs in this case.
View SolutionFor a reaction, A+2B→C, rate is given by +d[C]dt=k[A][B], hence, the order of the reaction is
View Solution
