For pair production i.e. for the production of electron and positron, the incident photon must have a minimum frequency of the order of
1018s−1
1021s−1
1025s−1
1030s−1
The correct Answer is:B
To solve the problem of determining the minimum frequency of a photon required for pair production (the creation of an electron and a positron), we will follow these steps:
Step 1: Understand the energy requirement for pair production
For pair production to occur, the energy of the incident photon must be at least equal to the combined rest mass energy of the electron and positron. The rest mass energy E can be expressed using the formula:
E=mc2
where m is the mass and c is the speed of light.
Step 2: Calculate the rest mass energy of an electron and positron
The rest mass of an electron (and positron) is approximately 0.511MeV. Therefore, the total rest mass energy for both particles is:
Etotal=2×0.511MeV=1.022MeV
Step 3: Convert the energy from MeV to Joules
To convert MeV to Joules, we use the conversion factor 1MeV=1.6×10−13J:
Etotal=1.022MeV×1.6×10−13J/MeV=1.6352×10−13J
Step 4: Relate energy to frequency using Planck's equation
The energy of a photon can also be expressed in terms of its frequency f using Planck's equation:
E=hf
where h is Planck's constant (h≈6.626×10−34J s).
Step 5: Solve for the minimum frequency
Rearranging the equation gives:
f=Eh
Substituting the values we calculated:
f=1.6352×10−13J6.626×10−34J s≈2.47×1020Hz
Step 6: Conclusion
The minimum frequency of the incident photon required for pair production is approximately 2.47×1020Hz.
For pair production to occur, the energy of the incident photon must be at least equal to the combined rest mass energy of the electron and positron. The rest mass energy E can be expressed using the formula:
E=mc2
where m is the mass and c is the speed of light.
The rest mass of an electron (and positron) is approximately 0.511MeV. Therefore, the total rest mass energy for both particles is:
Etotal=2×0.511MeV=1.022MeV
To convert MeV to Joules, we use the conversion factor 1MeV=1.6×10−13J:
Etotal=1.022MeV×1.6×10−13J/MeV=1.6352×10−13J
The energy of a photon can also be expressed in terms of its frequency f using Planck's equation:
E=hf
where h is Planck's constant (h≈6.626×10−34J s).
Rearranging the equation gives:
f=Eh
Substituting the values we calculated:
f=1.6352×10−13J6.626×10−34J s≈2.47×1020Hz
The minimum frequency of the incident photon required for pair production is approximately 2.47×1020Hz.
Similar Questions
In an ordianary atom, as a first approximation, the motion of the nucleus can be ignored. In a positronium atom a positronreplaces the proton of hydrogen atom. The electron and positron masses are equal and , therefore , the motion of the positron cannot be ignored. One must consider the motion of both electron and positron about their center of mass. A detailed analyasis shows that formulae of Bohr's model apply to positronium atom provided that we replace me by what is known reduced mass is me/2.
The orbital radius of the first excited level of postronium atom is
View SolutionIn an ordianary atom, as a first approximation, the motion of the nucleus can be ignored. In a positronium atom a positronreplaces the proton of hydrogen atom. The electron and positron masses are equal and , therefore , the motion of the positron cannot be ignored. One must consider the motion of both electron and positron about their center of mass. A detailed analyasis shows that formulae of Bohr's model apply to positronium atom provided that we replace me by what is known reduced mass is me/2.
If the Rydberg constant for hydrogen atom is R , then the Rydberg constant for positronium atom is
View Solution
Knowledge Check
In NO−3 ion, the number of bond pairs and lone pairs of electrons on nitrogen atom are
Thinking process
To solve this sequence we must know the structure of NO−3 ion i.e,
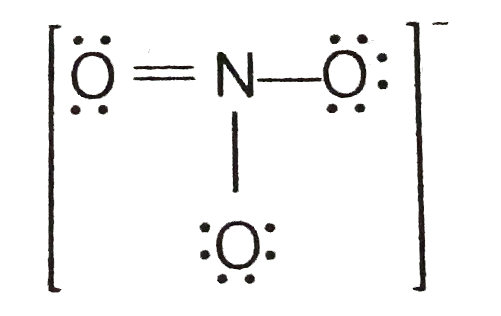
Then, cound the bond pairs and lone pairs of electron on nitrogen.A2,2B3,1C1,3D4,0
In an ordianary atom, as a first approximation, the motion of the nucleus can be ignored. In a positronium atom a positronreplaces the proton of hydrogen atom. The electron and positron masses are equal and , therefore , the motion of the positron cannot be ignored. One must consider the motion of both electron and positron about their center of mass. A detailed analyasis shows that formulae of Bohr's model apply to positronium atom provided that we replace me by what is known reduced mass is me/2.
When system de-excites from its first excited state to ground state, the wavelngth of radiation is
View SolutionFor production of beats the two souces must have
View SolutionWhat is the minimum product of the uncertainty in position and the uncertainty in momentum of a moving electron ?
View SolutionIn NO−3 ion, the number of bond pairs and lone pairs of electrons on nitrogen atom are
Thinking process
To solve this sequence we must know the structure of NO−3 ion i.e,

Then, cound the bond pairs and lone pairs of electron on nitrogen.
View Solution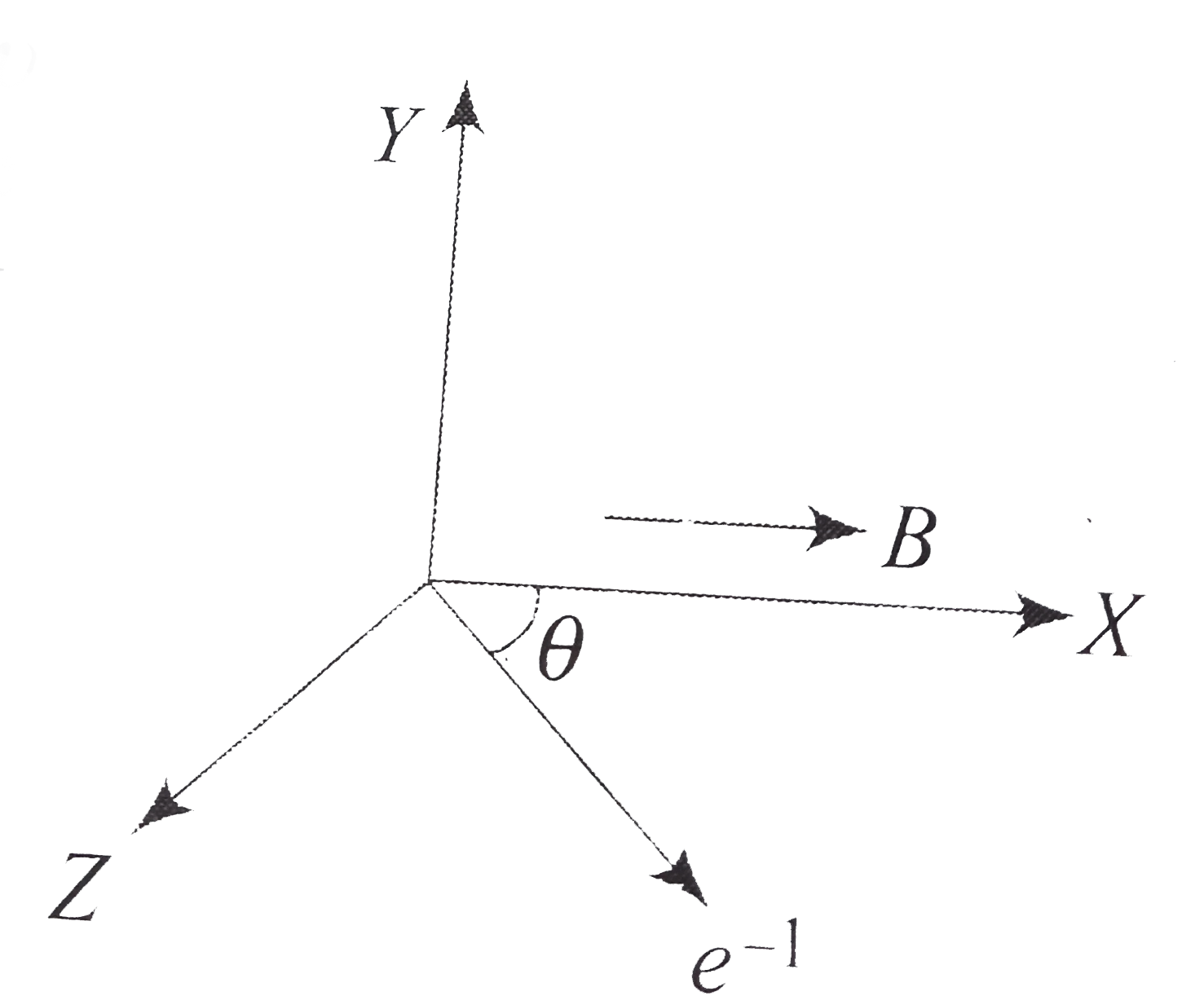
Light having photon energy hυ is incident on a metallic plate having work function ϕ to eject the electrons. The most energetic enectrons are then allowed to enter in a region of uniform magnetic field B as shown in Fig. The electrons are projected In X-Z plane making an angle θ with X-axis and magnetic field is →B=B0ˆi along X-axis maximum pitch of the helix described by an electron is found to be p. Take mass of electron as m and charge as q. Based on the above information, answer the following questions:
Q. The plot between X-coordinate of the location of electron as a function of time for different frequencies υ of the incident light is
View SolutionA high-energy gamma-photon may turn into an electron-positron pair in the field of heavy nuclei. What is the minimum energy of the gamma-photon?
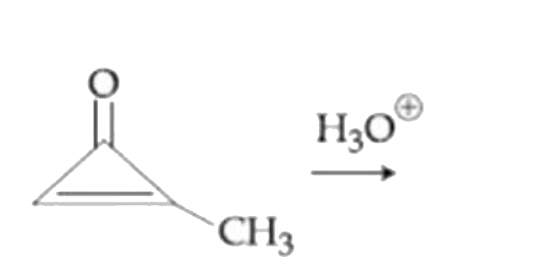
View SolutionThe major product in the following reaction is having how many pi electrons here ?
View Solution
