A motor pump lifts 6 tonnes of water from a height of 25 m to a height 35m from the ground floor in 20 seconds. The power of the pump (in kW) is [g=10ms−2]
3
12
1.5
6
The correct Answer is:A
To find the power of the pump, we can follow these steps:
Step 1: Understand the problem
We need to lift 6 tonnes of water from a height of 25 meters to a height of 35 meters. The difference in height (h) is 10 meters (35 m - 25 m). The time taken (t) for this lift is 20 seconds.
Step 2: Convert the mass of water to kilograms
1 tonne is equal to 1000 kg. Therefore, 6 tonnes of water is:
Mass (m)=6tonnes×1000kg/tonne=6000kg
Step 3: Calculate the work done (W)
The work done in lifting the water is given by the formula:
W=m⋅g⋅h
Where:
- m=6000kg (mass of water)
- g=10m/s2 (acceleration due to gravity)
- h=10m (height difference)
Substituting the values:
W=6000kg×10m/s2×10m
W=6000×10×10=600000J
Step 4: Calculate the power (P)
Power is defined as the work done per unit time:
P=Wt
Where:
- W=600000J (work done)
- t=20s (time taken)
Substituting the values:
P=600000J20s
P=30000W
Step 5: Convert power to kilowatts
1 kilowatt (kW) is equal to 1000 watts (W). Therefore:
P=30000W1000=30kW
Final Answer
The power of the pump is 30 kW.
---
We need to lift 6 tonnes of water from a height of 25 meters to a height of 35 meters. The difference in height (h) is 10 meters (35 m - 25 m). The time taken (t) for this lift is 20 seconds.
1 tonne is equal to 1000 kg. Therefore, 6 tonnes of water is:
Mass (m)=6tonnes×1000kg/tonne=6000kg
The work done in lifting the water is given by the formula:
W=m⋅g⋅h
Where:
- m=6000kg (mass of water)
- g=10m/s2 (acceleration due to gravity)
- h=10m (height difference)
W=6000kg×10m/s2×10m
W=6000×10×10=600000J
Power is defined as the work done per unit time:
P=Wt
Where:
- W=600000J (work done)
- t=20s (time taken)
P=600000J20s
P=30000W
1 kilowatt (kW) is equal to 1000 watts (W). Therefore:
P=30000W1000=30kW
The power of the pump is 30 kW.
Similar Questions
A body of mass 0.2 kg falls from a height of 10 m to a height of 6 m above the ground. Find the loss in potential energy taking place in the body.
[g=10ms−2]
View SolutionAn engine pumps up 100kg water through a height of 10m in 5s. If efficiency of the engine is 60%. What is the power of the engine? Takeg=10ms2.
View Solution
Knowledge Check
A crane lifts a mass of 100 kg to a height of 10 m in 20 s. The power of the crane is (Take g=10ms−2)
A100 WB200 WC250 WD500 W
A water pump raises 50 litres of water through a height of 25 m in 5 .Calculate the power of the pump required . (Take g=10 N kg−1 and density of water =1000 kg m−3)
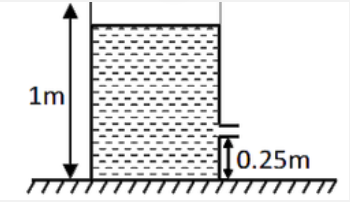
View SolutionIf a small orifice is made at a height of 0.25 m from the ground, the horizontal range of water stream will be : -
View SolutionA stone is dropped from the top of a tower of height 125 m. The distance travelled by it during last second of its fall is (g=10ms−2)
View SolutionA pump is required to lift 1000 kg of water per minute from a well 20 m deep and ejects at a speed of 20 m/s. The power of engine is
View SolutionAn engine pumps 400 kg of water through height of 10 m in 40 s. Find the power of the engine if its efficiency is 80% (Take ,g =10 ms−2).
View SolutionAn engine pumps 400 kg of water through height of 10 m in 40 s. Find the power of the engine if its efficiency is 80% (Take ,g =10 ms−2).
View SolutionAn engine pumps 400 kg of water through height of 10 m in 40 s. Find the power of the engine if its efficiency is 80% (Take ,g =10 ms−2).
View Solution
