Identify the function which represent a periodic motion.
loge(ωt)
sinωt+cosωt
e−ωt
eωt
The correct Answer is:B
To identify the function that represents periodic motion, we need to understand what periodic motion is. Periodic motion is defined as motion that repeats itself after a fixed period of time. Let's analyze each option provided in the question to determine which one represents periodic motion.
1. Understand Periodic Motion:
- Periodic motion is characterized by a function that repeats its values in regular intervals of time.
2. Evaluate the First Option: log(ωt):
- The function log(ωt) is a logarithmic function.
- Logarithmic functions are continuously increasing and do not repeat values.
- Therefore, this function does not represent periodic motion.
- Conclusion: This option is incorrect.
3. Evaluate the Second Option: sin(ωt) + cos(ωt):
- Both sine and cosine functions are periodic, with a period of 2π.
- The sum of two periodic functions with the same period is also periodic.
- Therefore, sin(ωt) + cos(ωt) represents a periodic motion with a period of 2π.
- Conclusion: This option is correct.
4. Evaluate the Third Option: e^(-ωt):
- The function e^(-ωt) is an exponential decay function.
- Exponential functions do not repeat values; they either grow or decay continuously.
- Therefore, this function does not represent periodic motion.
- Conclusion: This option is incorrect.
5. Evaluate the Fourth Option: e^(ωt):
- Similar to the previous option, e^(ωt) is an exponential growth function.
- Like the decay function, it does not repeat values and is not periodic.
- Therefore, this function does not represent periodic motion.
- Conclusion: This option is incorrect.
Final Answer:
The only function that represents periodic motion among the given options is sin(ωt) + cos(ωt).
- Periodic motion is characterized by a function that repeats its values in regular intervals of time.
- The function log(ωt) is a logarithmic function.
- Logarithmic functions are continuously increasing and do not repeat values.
- Therefore, this function does not represent periodic motion.
- Conclusion: This option is incorrect.
- Both sine and cosine functions are periodic, with a period of 2π.
- The sum of two periodic functions with the same period is also periodic.
- Therefore, sin(ωt) + cos(ωt) represents a periodic motion with a period of 2π.
- Conclusion: This option is correct.
- The function e^(-ωt) is an exponential decay function.
- Exponential functions do not repeat values; they either grow or decay continuously.
- Therefore, this function does not represent periodic motion.
- Conclusion: This option is incorrect.
- Similar to the previous option, e^(ωt) is an exponential growth function.
- Like the decay function, it does not repeat values and is not periodic.
- Therefore, this function does not represent periodic motion.
- Conclusion: This option is incorrect.
The only function that represents periodic motion among the given options is sin(ωt) + cos(ωt).
Topper's Solved these Questions
- BOOK - PHYSICS WALLAHCHAPTER - OSCILLATIONS EXERCISE - LEVEL-228videos
OSCILLATIONS
- BOOK - PHYSICS WALLAHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - NEET PAST 5 YEARS QUESTIONS12videos
MOVING CHARGES AND MAGNETISM
- BOOK - PHYSICS WALLAHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTS EXERCISE - NEET PAST 5 YEARS QUESTIONS16videos
RAY OPTICS AND OPTICAL INSTRUMENTS
Similar Questions
Knowledge Check
- Question 1 - Select One
Identify function which represent periodic motion
AeωtBloge(ωt)Csin(ωt)+cos(ωt)De−ωt - Question 2 - Select One
Which of the following functions of time represent periodic motion ?
Asinωt+cosωt,Be−ωtClog(ωt)DNone of these - Question 3 - Select One
Identify the correct equation which represents photosynthesis.
A6CO2+6H2O ----- C6H12O6+6O2B6CO2+6H2O ------- C12H22O11+6O2C6CO2+6H2O ------ C6H12O6D6CO2+6H2O ------ C22H33O12+7O2
Which of the following functions of time represents (a) periodic motion, (b) non-periodic motion and (c ) harmonic motion ?
find the period of each periodic motion. [ω is any positive constant]
(i) sin2ωt+cos2ωt
(ii) cosωt+2sin2πt+3cos3πt
(iii) cos2ωt
(iv) sin(2ωt+π/3)View SolutionDoes the function y=cos2ωt represent a periodic of a simple harmonic motion? What is the period of the motion?
View SolutionDoes the function y=sin2ωt represent a periodic or a simple harmonic motion ? What is the period of the motion ?
View SolutionIdentify the structure which represents homology in the following picture.
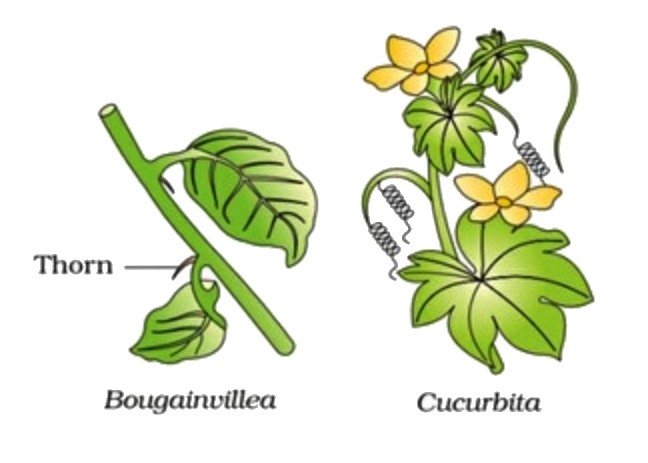 View Solution
View SolutionThe funtion of time representing a simple harmonic motion with a period of πω is :
View Solution

