When 5 children from class A join Class B, the number of children in both classes is he same. If 25 children from B, join A, then the number of children in A becomes double the number of children in B. The ratio of the number of children in A to those in B is.
जब कक्षा A के 5 बच्चे कक्षा B में शामिल होते हैं, तो दोनों कक्षाओं के बच्चों की संख्या समान होती है। यदि B के 25 बच्चे A से जुड़ते हैं, तो B में बच्चों की संख्या दोगुनी हो जाती है। B के बच्चों की संख्या A में उन बच्चों की संख्या का अनुपात है।
To solve the problem, we will define the number of children in Class A as x and the number of children in Class B as y. We will then set up equations based on the information given in the problem.
Step 1: Set up the first equation
When 5 children from Class A join Class B, the number of children in both classes becomes equal. Therefore, we can write the equation:
x−5=y+5
This simplifies to:
x−y=10(Equation 1)
Step 2: Set up the second equation
Next, when 25 children from Class B join Class A, the number of children in Class A becomes double the number of children in Class B. This gives us the equation:
x+25=2(y−25)
Expanding this, we get:
x+25=2y−50
Rearranging gives us:
x−2y=−75(Equation 2)
Step 3: Solve the equations
Now we have two equations:
1. x−y=10
2. x−2y=−75
We can solve these equations simultaneously. From Equation 1, we can express x in terms of y:
x=y+10
Substituting this expression for x into Equation 2:
(y+10)−2y=−75
This simplifies to:
10−y=−75
Thus:
−y=−75−10
−y=−85⇒y=85
Step 4: Find x
Now substituting y=85 back into Equation 1 to find x:
x−85=10
x=95
Step 5: Find the ratio
Now we have x=95 and y=85. The ratio of the number of children in Class A to those in Class B is:
xy=9585=1917
Final Answer
The ratio of the number of children in Class A to those in Class B is 19:17.
---
When 5 children from Class A join Class B, the number of children in both classes becomes equal. Therefore, we can write the equation:
x−5=y+5
This simplifies to:
x−y=10(Equation 1)
Next, when 25 children from Class B join Class A, the number of children in Class A becomes double the number of children in Class B. This gives us the equation:
x+25=2(y−25)
Expanding this, we get:
x+25=2y−50
Rearranging gives us:
x−2y=−75(Equation 2)
Now we have two equations:
1. x−y=10
2. x−2y=−75
x=y+10
(y+10)−2y=−75
This simplifies to:
10−y=−75
Thus:
−y=−75−10
−y=−85⇒y=85
Now substituting y=85 back into Equation 1 to find x:
x−85=10
x=95
Now we have x=95 and y=85. The ratio of the number of children in Class A to those in Class B is:
xy=9585=1917
The ratio of the number of children in Class A to those in Class B is 19:17.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Children of class one and two
Alearnt fast through abstract experiencesBlearn fast through concrete experiencesClearn fast by readingDlearn fast by writing - Question 2 - Select One
Children of class one and two
Alearnt fast through abstract experiencesBlearn fast through concrete experiencesClearn fast by readingDlearn fast by writing - Question 3 - Select One
The following table shows the number of children in each house of a society.
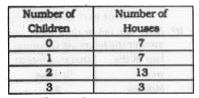
What is the average number of children per house ?AA)1.65BB)1.4CC)1.9DD)1.15
The number of boys in a class is three times the number of girls. Which of the following numbers cannot represent the total number of children in the class?
View SolutionThere are 40 children in a playground. If the number of girls is 25 and the remaining are boys, find the ratio of:
The number of boys to the number of children.View SolutionThe number of girls in a class is one third of the number of boys. Which one of the following numbers cannot represent the total number of children in the class?
View SolutionMostly children find class rooms in India
View Solution______is the total number of children of age group 6-10 attending school as a percentage of total number of children in the same age group
View Solution


