The length of a side of an equilateral triangle is 8 cm. The area of the region lying between the circum circle and the incircle of the triangle is (use: π=227)
एक समबहु त्रिकोण के भुजा की लंबाई 8 से.मी. है। त्रिकोण के अर्त्तवृत्त और परिवृत्त के मध्य स्थित क्षेत्र का क्षेत्रफल क्या है? (प्रयोग करे: π=227)
5017cm2
5027cm2
7517cm2
7527cm2
To find the area of the region lying between the circumcircle and the incircle of an equilateral triangle with a side length of 8 cm, we will follow these steps:
Step 1: Calculate the circumradius (R) of the equilateral triangle.
The formula for the circumradius R of an equilateral triangle is given by:
R=a√3
where a is the length of the side of the triangle.
Substituting a=8 cm:
R=8√3 cm
Step 2: Calculate the inradius (r) of the equilateral triangle.
The formula for the inradius r of an equilateral triangle is given by:
r=a2√3
Substituting a=8 cm:
r=82√3=4√3 cm
Step 3: Calculate the area of the circumcircle.
The area Acircum of the circumcircle is given by the formula:
Acircum=πR2
Substituting R=8√3:
Acircum=π(8√3)2=π⋅643
Using π=227:
Acircum=227⋅643=22⋅6421=140821 cm2
Step 4: Calculate the area of the incircle.
The area Ain of the incircle is given by the formula:
Ain=πr2
Substituting r=4√3:
Ain=π(4√3)2=π⋅163
Using π=227:
Ain=227⋅163=22⋅1621=35221 cm2
Step 5: Calculate the area between the circumcircle and the incircle.
The area between the circumcircle and the incircle is given by:
Abetween=Acircum−Ain
Substituting the areas we calculated:
Abetween=140821−35221=1408−35221=105621=50.2857 cm2
Final Answer:
The area of the region lying between the circumcircle and the incircle of the triangle is approximately 50.29 cm2.
---
The formula for the circumradius R of an equilateral triangle is given by:
R=a√3
where a is the length of the side of the triangle.
R=8√3 cm
The formula for the inradius r of an equilateral triangle is given by:
r=a2√3
Substituting a=8 cm:
r=82√3=4√3 cm
The area Acircum of the circumcircle is given by the formula:
Acircum=πR2
Substituting R=8√3:
Acircum=π(8√3)2=π⋅643
Using π=227:
Acircum=227⋅643=22⋅6421=140821 cm2
The area Ain of the incircle is given by the formula:
Ain=πr2
Substituting r=4√3:
Ain=π(4√3)2=π⋅163
Using π=227:
Ain=227⋅163=22⋅1621=35221 cm2
The area between the circumcircle and the incircle is given by:
Abetween=Acircum−Ain
Substituting the areas we calculated:
Abetween=140821−35221=1408−35221=105621=50.2857 cm2
The area of the region lying between the circumcircle and the incircle of the triangle is approximately 50.29 cm2.
Topper's Solved these Questions
Similar Questions
What is the length of the radius of the circumcircle of the equilateral triangle, the length of whose side is 6√3 cm ?
एक समबाहु त्रिभुज जिसकी भुजा की लम्बाई 6√3 सेमी है, के परिवृत्त की त्रिज्या की लम्बाई कितनी होगी?
View SolutionPerimeter of an equilateral triangle is equal to the circumference of a circle. The ratio of their areas is (Use π=227) एक समभुज त्रिभुज का परिमाप एक वृत्त की परिधि के बराबर है। उनके क्षेत्रफल का अनुपात क्या है? (π=227 का प्रयोग करें)
View Solution
Knowledge Check
On decreasing each side of an equilateral triangle by 2 cm, there is a decrease of 4 √3 cm2 in its area. The length of each side of the triangle is
एक समभुज त्रिभुज की प्रत्येक भुजा को 2cm कम करने से उसके क्षेत्रफल में 4√3cm2 की कमी हो जाती है। त्रिभुज की प्रत्येक भुजा की लंबाई कितनी है?A8 cmB3 cmC5 cmD6 cm
If the length of a side of a square is equal to the diameter of a circle, then the ratio between the areas of square and circle is (π=227)
यदि किसी वर्ग की भुजा की लम्बाई किसी वृत्त के व्यास के बराबर है, तब वर्ग तथा वृत्त के क्षेत्रफल का अनुपात हैः
View SolutionIf the radius of the circumcircle of an equilateral triangle is 8 cm, then the measure of radius of its incircle is:
यदि एक समबाहु त्रिभुज के परिवृत्त की त्रिज्या 8 सेमी है, तो इसके अंतः वृत्त की त्रिज्या का मान ज्ञात करें |
View SolutionThe in-radius of a triangle is 6 cm, and the sum of the length of its sides is 50cm. The area of the triangle (in sq. cm) is
एक त्रिभुज को अंतः त्रिज्या 6 सेमी है, तथा इसके भुजाओं के लंबाई का योग 50 सेमी है। त्रिभुज का क्षेत्रफल (वर्ग सेमी में) ज्ञात करें।
View SolutionThe diagonal of a square is equal to the side of an equilateral triangle. If the area of the square is 18√3 sq.cm. What is the area (in cm2) of the equilateral triangle?
किसी वर्ग का विकर्ण एक समबाहु त्रिभुज की भुजा के बराबर है | यदि वर्ग का क्षेत्रफल 18√3 वर्ग सेमी है, तो समबाहु त्रिभुज का क्षेत्रफल ( वर्ग सेमी में ) ज्ञात करें |
View SolutionIf the perimeter of an isosceles right triangle is 8(√2+1) cm, then the length of the hypotenuse of the triangle is:
यदि समद्विबाहु समकोण त्रिभुज की परिधि 8(√2+1) सेमी है, तो त्रिभुज के विकर्ण की लंबाई है
View SolutionIn the given figure, PQR is an equilateral triangle with side as 12cm. S and T are the mid points of the sides PQ and PR respectively. What is the area (in cm2) of the shaded region?
दी गई आकृति में PQR एक समबाहु त्रिभुज है जिसकी भुजा 12 से.मी. हैं। S तथा T क्रमशः भुजा PQ तथा PR के मध्य बिन्दु है। छायांकित भाग का क्षेत्रफल (से.मी.2 में) क्या है?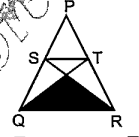
View SolutionThe side of a square is 6 cm. Find the area of the largest circle that can be drawn inside the square. (π=227)
एक वर्ग की भुजा 6 cm है | वर्ग के अंदर बनने वाले सबसे बड़े वृत्त का क्षेत्रफल कितना है?
View Solution
