B1 is a point on the side AC of ΔABC and B1B is joined. A line is drawn through a parallel to B1B meeting BC at A1 and another line is drawn through C parallel to B1B meeting AB produced at C1 The
1CC1−1AA1=1BB1
1CC1+1AA1=1BB1
1BB1−1AA1=1CC1
1AA1−1CC1=2BB1
Step by step video solution for B_(1) is a point on the side AC of DeltaABC and B_(1)B is joined. A line is drawn through a parallel to B_(1)B meeting BC at A_(1) and another line is drawn through C parallel to B_(1)B meeting AB produced at C_(1) The by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
P is the mid-point of side AB of parallelogram ABCD. A line drawn from B parallel to PD meets CD at Q and AD produce at R. Prove that :
(i) AR = 2BC (ii) BR= 2BQ
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
View Solution
Knowledge Check
B1 is a point on the side AC of ΔABC and B1B is joined. A line is drawn through a parallel to B1B meeting BC at A1 and another line is drawn through C parallel to B1B meeting AB produced at C1 The
A1CC1−1AA1=1BB1B1CC1+1AA1=1BB1C1BB1−1AA1=2CC1D1AA1−1CC1=2BB1Thet equatio of the line passing through (a, b) and parallel to the line xa+yb=1 is
Axa+yb=3Bxa+yb=2Cxa+yb=0Dxa+yb+2=0A variable line through (p,q) cuts the axes of co ordinates at A and B respectively. Lines are drawn through A parallel to y-axis and through B parallel to x-axis. If they meet at P, then locus of p is
Axp+yq=1Bpx+qy=1Cxq+yp=1Dqx+py=1
To constuct a triangle similar to a given ΔABC with its sides 73 of the corresponding side of ΔABC, draw a ray BX making acute angle with BC and X lies on the opposite side of A with respect of BC. The points B1,B2,…..,B7 are located at equal distances on BX, B3 is joined to C and then a line segment B6C' is drawn parallel to B3C, where C' lines on BC produced. Finally line segment A'C' is drawn parallel to AC.
View SolutionInternal bisector of ∠A of triangle ABC meets side BC at D. A line drawn through D perpendicular to AD intersects the side AC at E and the side AB at F. If a, b, c represent sides of ΔABC, then
View SolutionIf C is a point on the line segement joining A(-3,4) and B(2,1) such that AC = 2BC, then the coordinate of C is
View SolutionIn the given figure (not drawn to scalse ) , AG is parallel to CD and AG=27CD . The point B on AC is such that BC=27AC . If the line BG meets AD at F and the line through C is parallel to BG which meets AD at E , then find the value of FGEC .
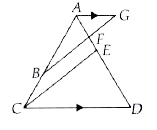
View SolutionA straight line through the point (1,1) meets the x-axis at 'A' and the y axis at 'B'. The locus of the mid point of AB is :
View Solution
