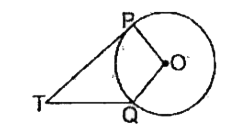
Let P and Q be two points on a circle with centre O. If two tan gents of the circle through P and O meet at A with ∠PAQ=48∘, then ∠APO is
48∘
60∘
96∘
66∘
Step by step video & image solution for Let P and Q be two points on a circle with centre O. If two tan gents of the circle through P and O meet at A with /_PAQ = 48^@, then /_APO is by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
P and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
View SolutionTwo tangents AP and AQ are drawn to a circle with centre O from an external point A, where P and Q are points on the circle. If the ∠PAQ=70∘, then the ∠AOP is equal to:
दो स्पर्शरेखा AP और AQ एक बाहरी बिंदु A से केंद्र O के साथ एक वृत्त में खींची जाती हैं, जहां P और Q वृत्त पर बिंदु होते हैं। यदि ∠PAQ=70∘, तो ∠AOP का मान है:
View Solution
Knowledge Check
PA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=40∘, then ∠OABis equal to:
A40∘B20∘C50∘D25∘P and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
A80∘B200∘C160∘D100∘PA and PB are tangents to a circle with centre O, from a point P outside the circle and A and B are points on the circle. If ∠APB=30∘, then ∠OAB is equal to :
AA) 40∘BB) 15∘CC) 50∘DD) 25∘
From a point P outside the circle with centre O, two tangents PA and PB are drawn to meet the circle at A and B respectively. If ∠APB=70∘, then ∠OAB is equal to :
केंद्र O वाले वृत्त के बाहर स्थित किसी बिंदु P से दो स्पर्श रेखाएं PA और PB खींची जाती हैं जो वृत्त से क्रमशः A और B मिलती हैं | यदि ∠APB=70∘ है, तो कोण OAB का मान ज्ञात करें |
View SolutionP and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=100∘ , then OAB is equal to:
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
View SolutionTP and TQ are tangents from T to the circle with centre O. Then is it possible to draw a circle through the points P, O, Q and T ?
View Solution