Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
Step by step video & image solution for Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
View SolutionThe length of the two sides of a right-angled triangle are equal Find the length of the hypotenuse
View Solution
Knowledge Check
- Question 1 - Select One
The hypotenuse of a right-angled isosceles triangle is 5 cm. The area of the triangle is (a) 5 cm2 (b) 6.25 cm2 (c) 6.5 cm2 (d) 12.5 cm2
A5 cm2B6.25 cm2C6.5 cm2D12.5 cm2
If the length of the hypotenuse of a right angled triangle is 10 cm, then what is the maximum area of such a right angled triangle?
View SolutionEquilateral triangles are drawn on the sides of a right triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
View SolutionTheorem 6.8 : In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
View SolutionA right angle triangle whose hypotenuse is c and its perpendicular sides are a and b. Three semicircles are drawn along the three sides of this triangle in such a way that the diameter of each semicircle is equal to the length of the respective side of the triangle. The semicircle drawn wiht the help of hypotenuse intersects the other two semicircles as shown in the concerned diagram. Find the area of the shaded region.
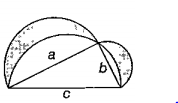 View Solution
View SolutionProve that is a right angle triangle, the square of the hypotenuse is equal the sum of the squares of other two sides.
View SolutionIf the sum of a side and hypotenuse of a right angled triangle is given then show that area of triangle will be maximum when the angle between side and the hypotenuse is π/3.
View SolutionProve that, in a right-angled triangle, the square of hypotenuse is equal to the sum of the square of remaining two sides.
View Solution
