In the figure, chord AB subtends an angle of 60°∘ at the centre of the circle of radius 3.5 cm. Find the (a) length of the arc APB (b) the area of the sector AOB (C) area of the minor segment (Shaded region) (use√3=1.73)
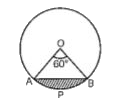
Step by step video & image solution for In the figure, chord AB subtends an angle of 60°^(@) at the centre of the circle of radius 3.5 cm. Find the (a) length of the arc APB (b) the area of the sector AOB (C) area of the minor segment (Shaded region) (usesqrt(3)=1.73) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In a circle of radius 6 cm, a chord of length 10 cm makes an angle of 110o at the centre of the circle. Find (i) the length of the arc AB , (ii) the area of the sector OAB .
View SolutionIn a circle of radius 7 cm , a chord makes an angle of 60∘ at the centre of the circle . Find (a) area of the circle (b) area of sector AOB and ( c) area of minor segment APB.
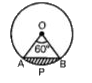
(Take √3=1.73)
View Solution
Knowledge Check
An arc subtended an angle 60∘ at the center of c circle of radius 6 cm , then length of minor and major arc
A2πand10πB10πand2πC8πand4πD4πand6πWhat is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm?
A8.5 cm2B8.75 cm2C7.75 cm2D125 cm2
Radius of a sector of a circle is 3.5 cm and length of its arc is 2.2 cm. Find the area of the sector.
View SolutionAn arc subtends an angle of 90o at the centre of the circle of radius 14 cm. Write the area of minor sector thus formed in terms of π .
View SolutionIn a circle of radius 5 cm an arc subtends an angle of 30∘, then find the area of the sector.
View SolutionIn a circle of radius 28 cm, an arc subtends an angle of 108∘ at the centre .
(a) Find the area of the sector.
(b) Find the length of the arc.
View SolutionIn a circle of radius 4 cm, an arc subtends an angle of 60∘ at the centre. Find the length of the arc.
View SolutionIn a circle of radius 21 cm, an arc subtends an angle of 60∘ at the centre. Find the length of the arc.
View Solution
