Case Study Based- 3
Applications of Parabolas-Highway Overpasses/Underpasses A highway underpass is parabolic in shape.

Parabola
A parabola is the graph that results from p(x)=ax2+bx+c
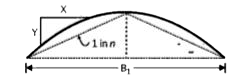
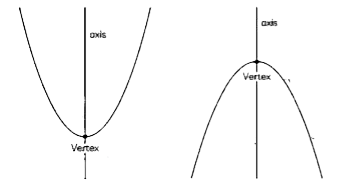
Parabolas are symmetric about a vertical line known as the Axis of Symmetry. The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the Vertex.
The highway overpass is represented graphically. Zeroes of a polynomial can be expressed graphically. Number of zeroes of polynomial is equal to number of points where the graph of polynomial
Intersect x-axis
Intersects y - axis
Intersects y axis or x- axis
None of these
Step by step video & image solution for Case Study Based- 3 Applications of Parabolas-Highway Overpasses/Underpasses A highway underpass is parabolic in shape. Parabola A parabola is the graph that results from p(x) = ax^(2)+bx+c Parabolas are symmetric about a vertical line known as the Axis of Symmetry. The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the Vertex. The highway overpass is represented graphically. Zeroes of a polynomial can be expressed graphically. Number of zeroes of polynomial is equal to number of points where the graph of polynomial by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Case Study Based- 3
Applications of Parabolas-Highway Overpasses/Underpasses A highway underpass is parabolic in shape.

Parabola
A parabola is the graph that results from p(x)=ax2+bx+c
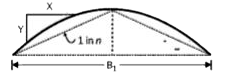
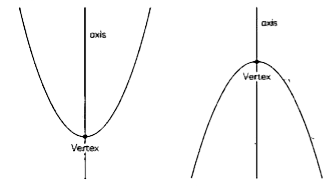
Parabolas are symmetric about a vertical line known as the Axis of Symmetry. The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the Vertex.
If the highway overpass is represented by x2−2x−8. Then its zeroes are
View SolutionCase Study Based- 3
Applications of Parabolas-Highway Overpasses/Underpasses A highway underpass is parabolic in shape.

Parabola
A parabola is the graph that results from p(x)=ax2+bx+c
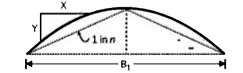
Parabolas are symmetric about a vertical line known as the Axis of Symmetry. The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the Vertex.
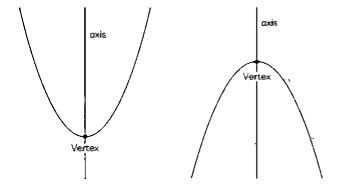
Graph of a quadratic polynomial is a
View SolutionCase Study Based- 3
Applications of Parabolas-Highway Overpasses/Underpasses A highway underpass is parabolic in shape.

Parabola
A parabola is the graph that results from p(x)=ax2+bx+c
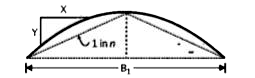
Parabolas are symmetric about a vertical line known as the Axis of Symmetry. The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the Vertex.

The representation of Highway Underpass whose one zero is 6 and sum of the zeroes is 0, is
View SolutionCase Study Based- 3
Applications of Parabolas-Highway Overpasses/Underpasses A highway underpass is parabolic in shape.

Parabola
A parabola is the graph that results from p(x)=ax2+bx+c
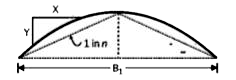
Parabolas are symmetric about a vertical line known as the Axis of Symmetry. The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the Vertex.
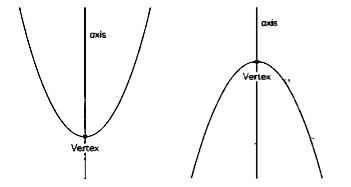
The number of zeroes that polynomial f(x)=(x−2)2+4 can have is:
View SolutionWrite the axis of symmetry of the parabola y2=x.
View SolutionThe point on the axis of symmetry that bisects the parabola is called the "vertex”, and it is the point where the curvature is greatest.
View SolutionIs the parabola y2=4x symmetrical about x-axis ?
View SolutionParabolas having their vertices at the origin and foci on the x-axis.
View SolutionShow that the locus of the mid point of chords of a parabola passing through the vertex is a parabola
View SolutionThe locus of the mid-point of the chords of the parabola y2=4ax which pass through the vertex is the parabola y2=2ax.
View Solution
