In CERN , some work is carried out for developing an accurate and fast numerical method that can calculate natural gas flow in a pipeline under non isothermal steady -state conditions .
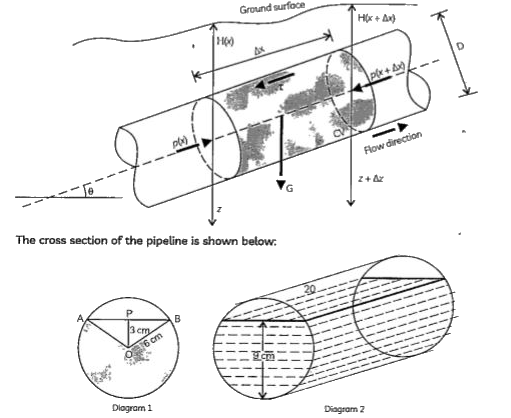
In Diagram 1, O is the centre of the circle of radius 6 cm and P is the mid -point of the chord AB .The length OP is 3 cm.
The area (in sq cm ) of ΔAOB is :
5.2
10.4
15.6
20.8
Step by step video solution for In CERN , some work is carried out for developing an accurate and fast numerical method that can calculate natural gas flow in a pipeline under non isothermal steady -state conditions . In Diagram 1, O is the centre of the circle of radius 6 cm and P is the mid -point of the chord AB .The length OP is 3 cm. The area (in sq cm ) of DeltaAOB is : by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In CERN , some work is carried out for developing an accurate and fast numerical method that can calculate natural gas flow in a pipeline under non isothermal steady -state conditions .
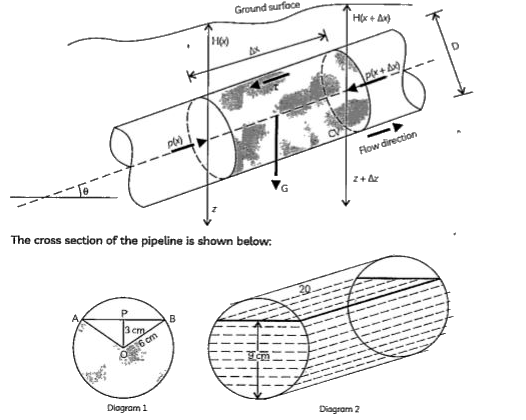
In Diagram 1, O is the centre of the circle of radius 6 cm and P is the mid -point of the chord AB .The length OP is 3 cm.
The measure of ∠AOB is :A60∘B75∘C120∘D135∘ - Question 2 - Select One
O is the centre of the circle of radius 6 cm and P is the mid -point of a chord AB .The length OP is 3 cm. The area (in sq cm ) of △AOB is :
A26πB24πC20πD18π - Question 3 - Select One
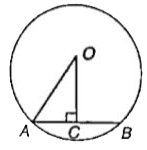
In the given figure, O is the centre of a circle of radius 13 cm and AB is a chord perpendicular to OD. If CD = 8 cm, then what is the length (in cm) of AB?
 AA)6 cmBB)12 cmCC)24 cmDD)28cm
AA)6 cmBB)12 cmCC)24 cmDD)28cm
In the given figure, O is the centre of the circle. Radius of the circle is 17 cm. lf OC=8cm, then the length of the chord AB is :
 View Solution
View SolutionThe length of a chord of a circle of radius 10 cm is 12 cm. Find the distance of the chord from the centre of the circle.
View SolutionIn a circle of radius 10 cm, a chord is at a distance of 6 cm from the centre. The length of chord is
View SolutionThe length of the radius of a circle with centre O is 5 cm and the length of the chord AB is 8 cm. The distance of the chord AB from the point O is
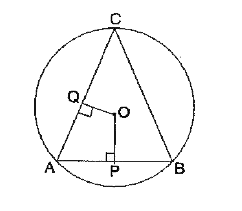
View SolutionO is the centre of the circle ABC, radius 5 cm, AB = 8 cm, AC = 6 cm. Calculate the lengths of the perpendiculars OP, OQ from O to AB, AC.
 View Solution
View Solution


