Find 7π6 in degree measure.
210∘
300∘
310∘
200∘
The correct Answer is:A
To convert the angle 7π6 radians into degrees, we can use the conversion factor that 180∘ is equivalent to π radians. Here’s how to do it step by step:
Step 1: Write the conversion formula
The formula to convert radians to degrees is:
Degrees=Radians×180∘π
Step 2: Substitute the given value
Now, substitute 7π6 into the formula:
Degrees=7π6×180∘π
Step 3: Simplify the expression
Now, we can simplify the expression. The π in the numerator and denominator cancels out:
Degrees=7×180∘6
Step 4: Calculate the multiplication
Now, calculate 7×180:
7×180=1260
Step 5: Divide by 6
Now, divide 1260 by 6:
Degrees=12606=210∘
Final Answer
Thus, 7π6 radians is equal to 210∘.
---
The formula to convert radians to degrees is:
Degrees=Radians×180∘π
Now, substitute 7π6 into the formula:
Degrees=7π6×180∘π
Now, we can simplify the expression. The π in the numerator and denominator cancels out:
Degrees=7×180∘6
Now, calculate 7×180:
7×180=1260
Now, divide 1260 by 6:
Degrees=12606=210∘
Thus, 7π6 radians is equal to 210∘.
Similar Questions
Knowledge Check
- Question 1 - Select One
Find 5π3 in degree measure.
A210∘B300∘C310∘D200∘ - Question 2 - Select One
Find the radian measures corresponding to the following degree measures:
A25∘B−47∘30′C240∘D520∘ - Question 3 - Select One
In the adjoining circle C(O,r)the degree measure of minor arc AB=130∘ Find the degree measure of major arc.
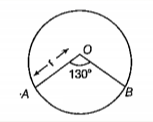 A230∘B260∘C310∘Dnone of the above
A230∘B260∘C310∘Dnone of the above
Convert the following radian into degree measure5π3
View SolutionConvert 6 radians into degree measure.
View Solution(a) Find the radian measure corresponding to the following measures:
(i) (I) 35∘ (ii) -45∘30' (iii) (I) 150g (iv) 70g50'
(b) Find the degree measure corresponding to the following radian measures:
(i) 6
(ii) 5π3View SolutionIn the adjoining circle C(O,r)the degree measure of minor arc AB=130∘ Find the degree measure of major arc.
 View Solution
View Solution2. Find the corresponding degree measurement of the following radian measurements
View Solution

