Coefficient of performance of an ideal refrigerator working between temperature T1 and T2(T1>T2) is
β=T2T1−T2
β=T2T1+T2
β=T1T1−T2
β=T1T1+T2
The correct Answer is:C
Similar Questions
Knowledge Check
The efficiency of an ideal heat engine working between the temperatureT1 and T2(T1>T2) is
A1−T1T2B1−T2T1C1+T2T1DT2T1The efficiency of a carnot engine working between temperature T1 and T2 is η. It will be also η if it works between temperatures
AT1+10 and T2+10BT1−10 and T2−10C2T1 and 2T2Din all the above casesDetermine coefficient of performance of given temperature limit.
T1=27∘C [outside fridge]
T2=−23∘C [inside fridge]A4B5C6D7
Two ideal Carnot engines operate in cascade (all heat given up by one engine is used by the other engine to produce work) between temperatures, T1andT2. The temperature of the hot reservoir of the first engine is T1 and the temperature of the cold reservoir of the second engine is T2. T is temperature of the sink of first engine which is also the source for the second engine. How is T related to T1andT2, if both the engines perform equal amount of work?
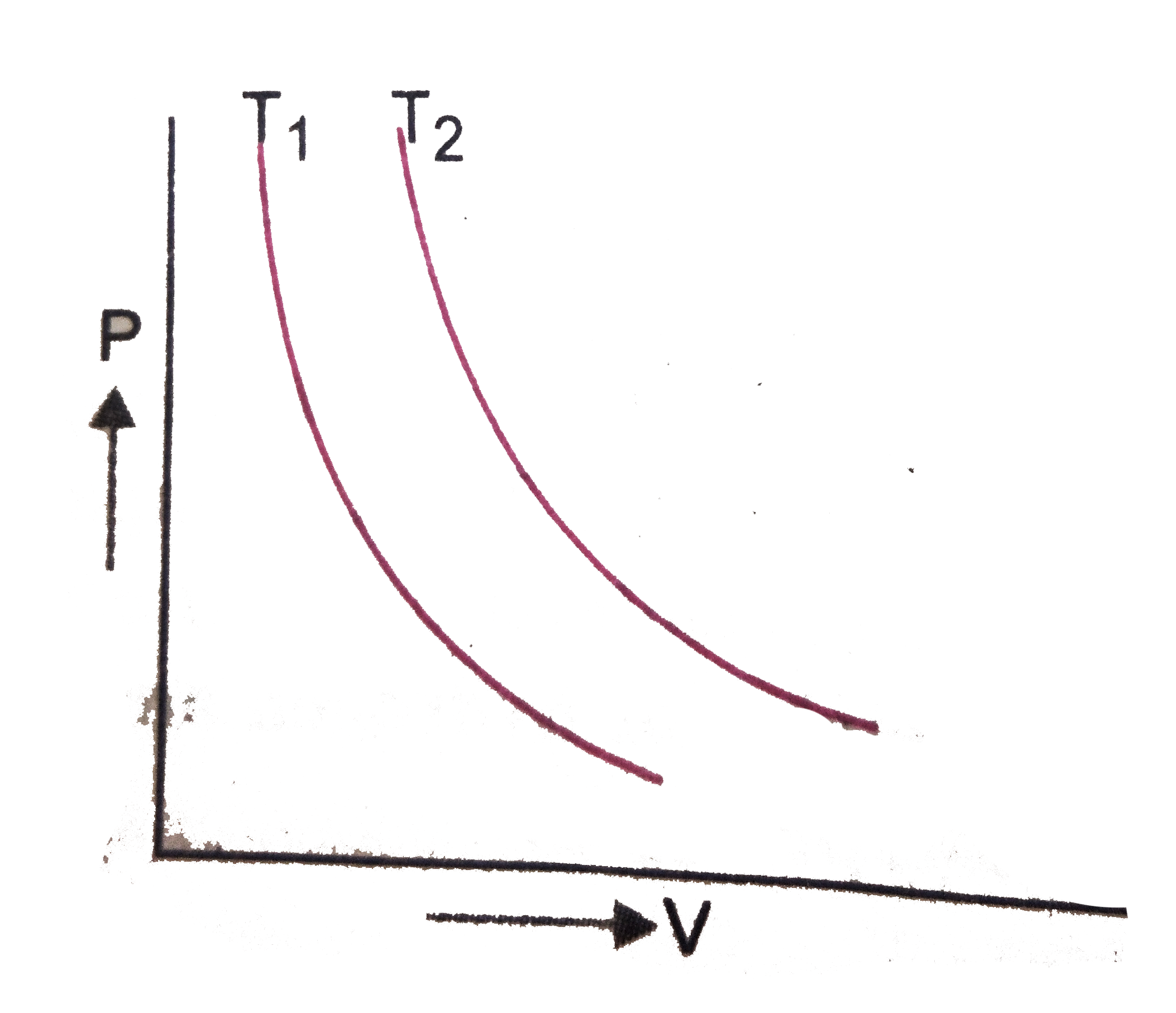
View SolutionIsothermal curves for a given mass of gas are shown at two different temperture T1andT2 in Fig. State whether T1>T2orT2>T1. Justify your answer.
View SolutionFigure shows graphs of pressure versus density for an ideal gas at two temperatures T1 and T2 Then

View SolutionThe efficiency of a Carnot engine which operates between the two temperatures T1=500K and T2=300K is
View SolutionTwo ideal Carnot engines operate in cascade (all heat given up by one engine is used by the other engine to produce work) between temperatures, T1andT2. The temperature of the hot reservoir of the first engine is T1 and the temperature of the cold reservoir of the second engine is T2. T is temperature of the sink of first engine which is also the source for the second engine. How is T related to T1andT2, if both the engines perform equal amount of work?
View Solution

 .
.