The speed on string with tension T and linear mass density μ is -
V=√Tμ
V=√Bρ
V=√Yρ
None of these
The correct Answer is:A
Similar Questions
The speed of transverse wave v in a stretched string depend on length tension T in the string and liner mass density (mass per unit length). μ. Find the relation using method of dimensions.
View SolutionConsider an elastic string stretched befween two fixed ends A and B as sbown in figure. The speed of transverse waves in the string is v and its linear mass density is μ. The string is plucked and held in a triangular form with maximum height h⟨L at its middle point. At t=0, the plucked string is released. AIl effects due to gravity may be neglected. Let T be the period of string's vibrations. If total mechanical energy of the vibrating string can be expressed either Pμv2h2/(L) or QμLh2/(T2) where P and Q are integer. Find P×Q.
'(##CEN_KSR_PHY_JEE_C17_E01_035_Q11##)'
View Solution
Knowledge Check
In (Q. 24.) the tension in string is T and the linear mass density of string is μ. The ratio of magnitude of maximum velocity of particle and the magnitude of maximum acceleration is
A12π√μl2TB2π√μl2TC12π√Tμl2D14π√μl2TWhich of the following is not the law of a stretched string ? ( n , l , T and m are frequency of vibration , length of vibrating string , tension in string and linear mass density , respectively .)
An∝1√TBn∝1lCn∝1√mDAll the aboveA mass m is suspended from the ceiling by a string with variable linear mass density (μ).A wave pulse is produced at the top of an oscillator which travels from top to bottom with constant wave speed. (x axis is positive downwards). Then.
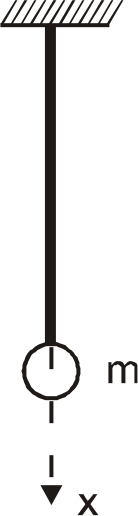 Adμdx>0Bdμdx<0Cdμdx=constantDdμdx=0
Adμdx>0Bdμdx<0Cdμdx=constantDdμdx=0
A mass m is suspended from the ceiling by a string with variable linear mass density (μ).A wave pulse is produced at the top of an oscillator which travels from top to bottom with constant wave speed. (x axis is positive downwards). Then.
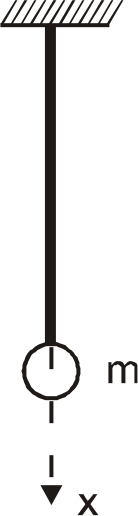
View SolutionA string of length 1m fixed at both ends is vibrating in 3rd overtone. Tension in string is 200N and linear mass density is 5 gmin. Frequency of these vibrations is (in Hz ).
View SolutionA transverse periodic wave on a string with a linear mass density of 0.200 kg/m is described by the following equation y=0.05sin(420t−21.0x)
where x and y are in metres and t is in seconds.The tension in the string is equal to :
View SolutionA transverse periodic wave on a string with a linear mass density of 0.200 kg/m is described by the following equation y=0.05sin(420t−21.0x)
where x and y are in metres and t is in seconds.The tension in the string is equal to :
View SolutionA transverse periodic wave on a string with a linear mass density of 0.200kg/m is described by the following equation
y=0.05sin(420t−21.0x)
where x and y are in meters and t is in seconds.
The tension in the string is equal to :
View Solution
