△ABC একটিত্রিভুজযায় BC বাহুরমধ্যবিন্দুহলো D এবং E হল AD এরমধ্যবিন্দু।প্রমাণকরো △BED -এরক্ষেত্রফল=14×△ABC -এরক্ষেত্রফল।
Step by step video & image solution for triangleABC একটিত্রিভুজযায় BC বাহুরমধ্যবিন্দুহলো D এবং E হল AD এরমধ্যবিন্দু।প্রমাণকরো triangleBED -এরক্ষেত্রফল=1/4xx triangleABC -এরক্ষেত্রফল। by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
বিশ্লেষণ করো : a2+8a+12
03:34View Solutionনিন্মলিখিত দৈর্ঘ্য ও প্রস্থবিশিষ্ট আয়তক্ষেত্রটির ক্ষেত্রফল বর্গমিটার নির্ণয় করো - দৈর্ঘ্য 720 সেমি , প্রস্থ 25 সেমি ।
03:44View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).
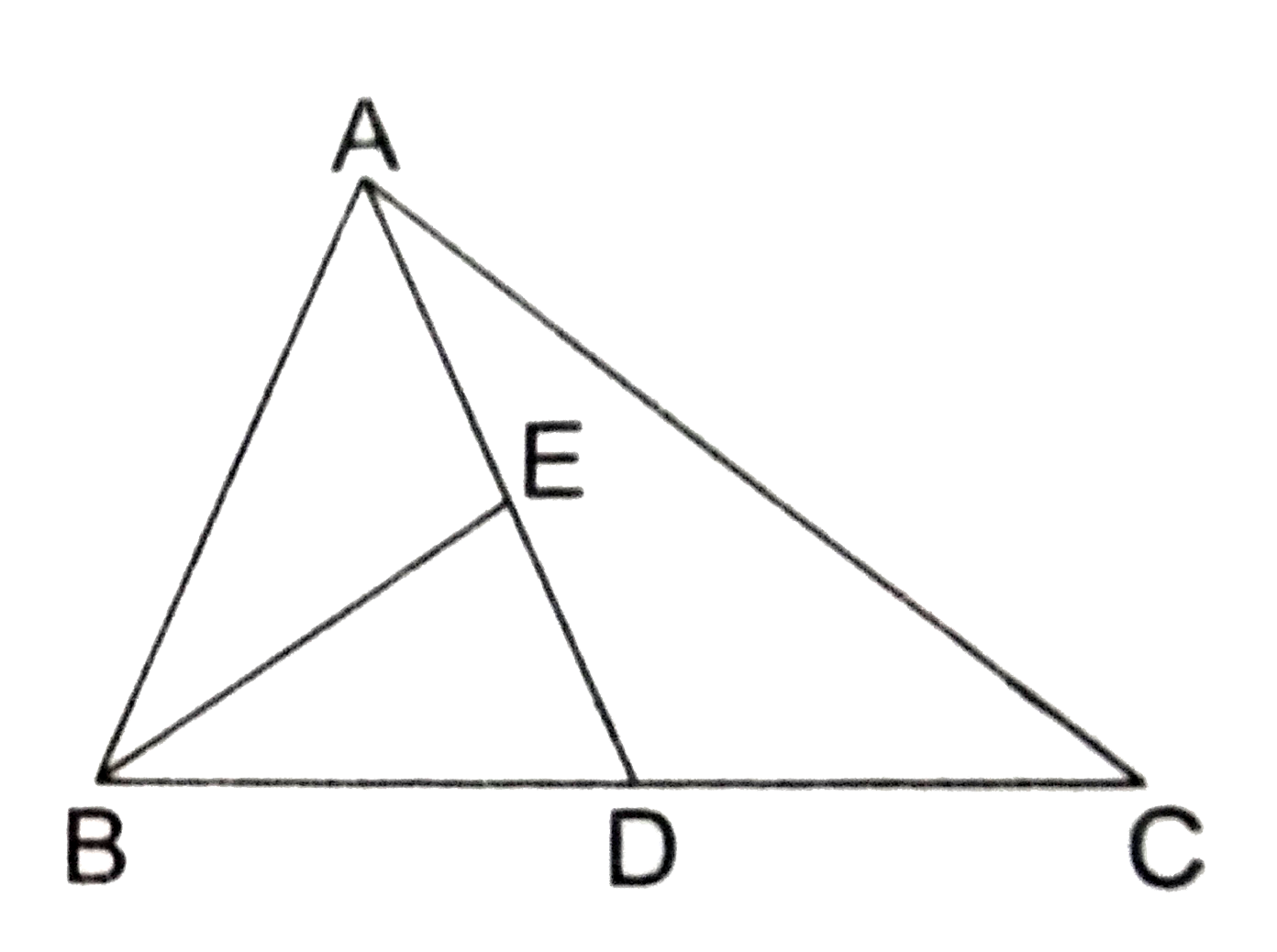 02:07View Solution
02:07View SolutionD is the midpoint of side BC of △ABC and E is the midpoint of BD. If O is the midpoint of AE,
prove that ar(△BOE)=18ar(△ABC).
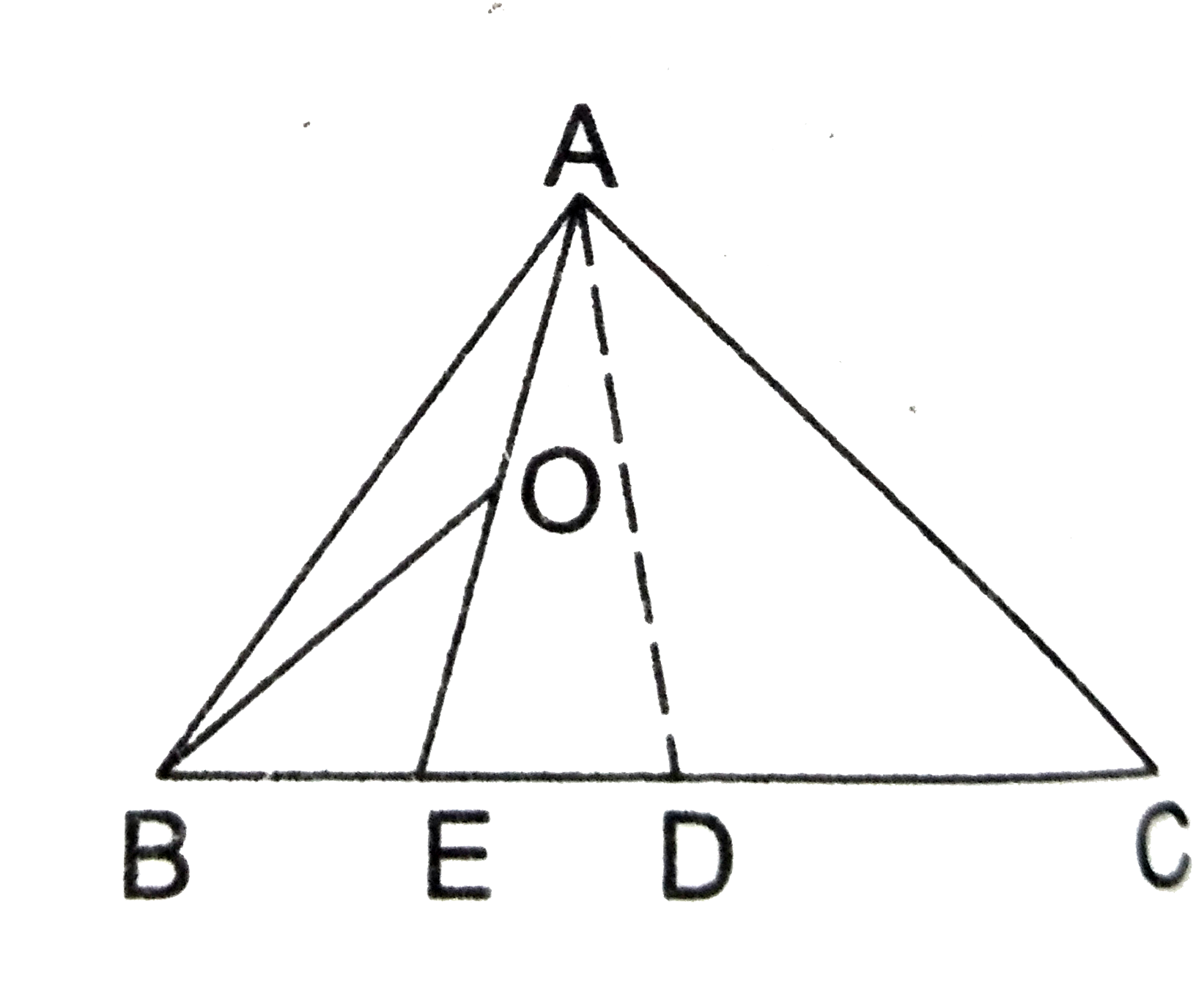 01:14View Solution
01:14View SolutionIn △ABC, if D is the midpoint of BC and E is the midpoint of AD then ar(△BED) = ?
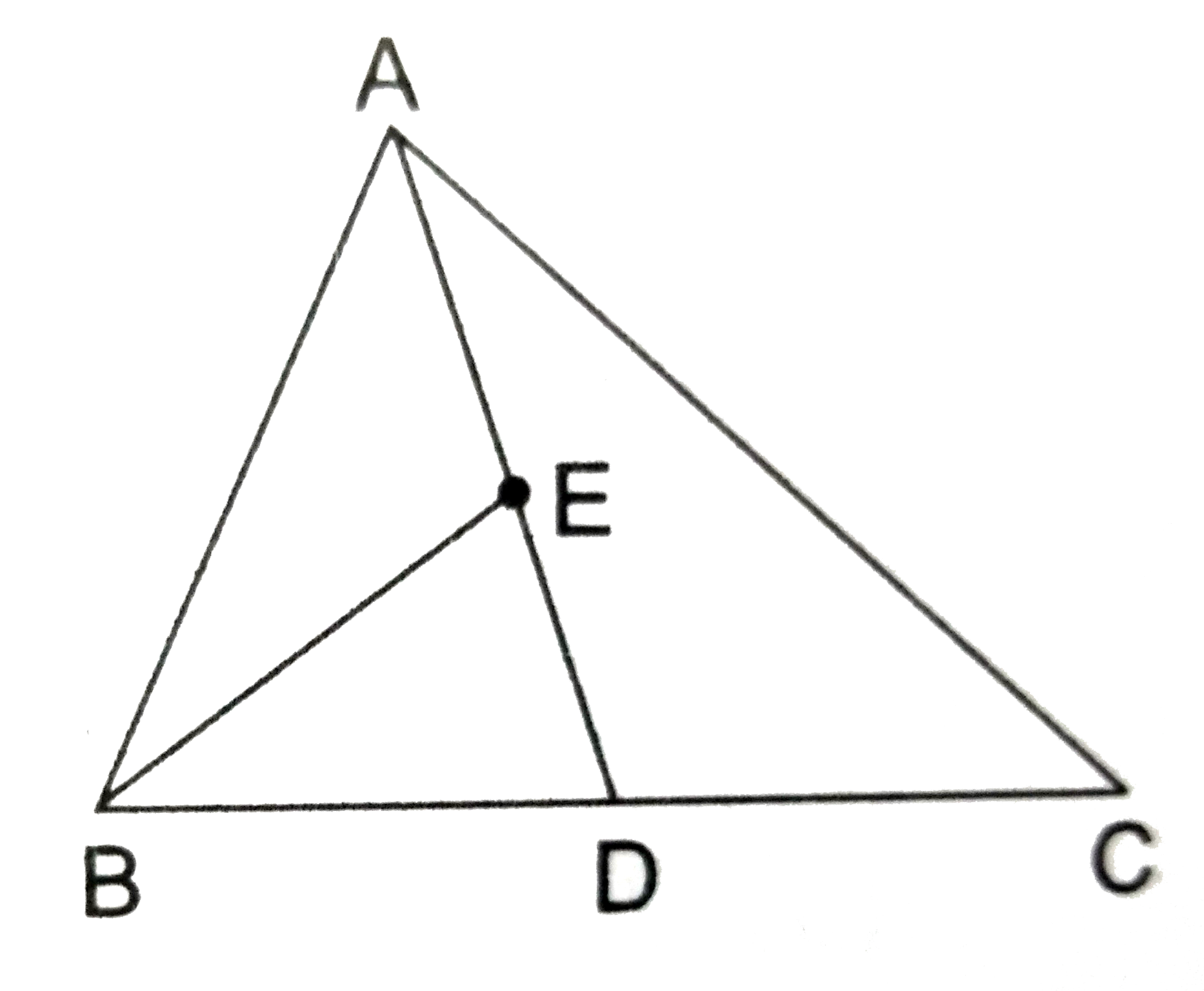 02:45View Solution
02:45View SolutionIn the given Fig., D and E are points on sides AB and CA of triangleABC such that triangleB= angleAED. Show that triangleABC ~ triangleAED .
06:58View SolutiontriangleABC , In BC the lump of BC is AD (see Figure). As AB = AC triangleABC Show that an isosceles triangle.
07:57View SolutionD, E and F are respectively the mid-points of sides AB. BC and CA of △ABC. Find the ratio of the areas of △DEF and △ABC.
08:56View SolutionIn △ABC, point D lies on side BC. E is the midpoint of AD. Prove that,
ar(EBC)=12ar(ABC)03:57View SolutionD,E and F are respectively the mid-points of sides AB,BC and CA of △ABC.Find the ratio of the areas of △DEFand△ABC.
04:48View SolutionD and E are two points on the sides AC and AB respectively of △ABCsuch that △ADE~△ABC.If AD=1.9cm,AE=3.6cm.BE=2.1cm.and BC=8.4 cm.find DE.
02:45View SolutionIn ∠ABC, D is a point on side BC, △ABC such that AD. AC (see figure).
 08:01View Solution
08:01View SolutionIn △ABC, D and E are two points on AB and AC such that DE || BC and AD : BD = 3 : 2, then DE : BC =
01:10View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (triangleBED)=1/4 ar( triangleABC ).
01:47View SolutiontriangleABC The bisector of A of A cuts BC at D and the circumcircle of the triangle at E, then
01:26View Solution

