5 সেমি ব্যাসার্ধবিশিষ্ট বৃত্তের AB এবং AC হলো দুটি জ্যা। AB=AC=6 সেমি হলে, BC = ?
Step by step video & image solution for 5 সেমি ব্যাসার্ধবিশিষ্ট বৃত্তের AB এবং AC হলো দুটি জ্যা। AB = AC = 6 সেমি হলে, BC = ? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
একটি শঙ্কুর উচ্চতা 24 সেমি এবং তির্যক উচ্চতা 25 সেমি। শঙ্কুটির সমান আয়তনবিশিষ্ট একটি লম্ববৃত্তাকার চোঙের উচ্চতা 15 সেমি হলে চোংটি ভূমির ব্যাস নির্ণয় করো।
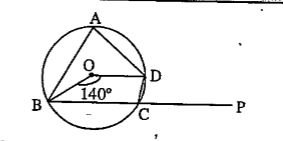
View Solutionচিত্রে O কেন্দ্র ∠BOD=140∘। BC বাহুকে P পর্যন্ত বর্ধিত করলে ∠BAD ও ∠DCB =?
View Solutionगुणनखंड ज्ञात कीजिए- ab+bc+a2+ac
View Solution5 सेमी. त्रिज्या वाले एक वृत्त कि दो जिवाएँ AB तथा AC इस प्रकार हैं कि AB=AC=6 सेमी. जीवा BC की लम्बाई ज्ञात करो।
View Solutionপ্রমান করো যে,
∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac −acc2+aca2+abb2+ab −ab∣∣ ∣ ∣∣=(ab+bc+ca)3
View Solutionif AB=5 and AC=12 then BC cannot be
View Solutionif AB=5 and AC=12 then BC cannot be
View Solutiona2+bc+ab+ac= ?
View Solution|→α|=4, abs(vecbeta) =3এবংabs(vecalphaxxvecbeta) =6 হলে, vecalpha ও vecbeta ভেক্টর দুটির অন্তর্গত কোণ হবে—
View SolutionNow draw a triangle ABC and measure its sides. Find the sum of the sides AB + BC, BC + AC and AC + AB, compare it with the length of the third side. What do you observe?
You will observe that AB + BC > AC, BC + AC > AB and AC + AB > BC.
View SolutionNow draw a triangle ABC and measure its sides. Find the sum of the sides AB + BC, BC + AC and AC + AB, compare it with the length of the third side. What do you observe?
You will observe that AB + BC > AC, BC + AC > AB and AC + AB > BC.
View SolutionNow draw a triangle ABC and measure its sides. Find the sum of the sides AB + BC, BC + AC and AC + AB, compare it with the length of the third side. What do you observe?
You will observe that AB + BC > AC, BC + AC > AB and AC + AB > BC.
View SolutionUsing the properties of determinants show that : ∣∣ ∣ ∣∣⎡⎢⎣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab⎤⎥⎦∣∣ ∣ ∣∣=(ab+bc+ca)3
View SolutionIn a circle of radius 5 cm, AB and AC are two chords, such that AB = AC = 6 cm. Find the length of the chord BC.
View Solution|[-bc, b^2+bc, c^2 +bc],[a^2+ac,-ac,c^2+ac],[a^2+ab,b^2+ab,-ab]|=64 . then (ab+bc+ac) is
View Solution
