O কেন্দ্রীয় বৃত্তে QR একটি জ্যা। Q এবং R বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে P বিন্দুতে ছেদ করে। QM বৃত্তটির ব্যাস হলে, প্রমাণ করো যে, ∠QPR=2∠RQM.
Step by step video & image solution for O কেন্দ্রীয় বৃত্তে QR একটি জ্যা। Q এবং R বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে P বিন্দুতে ছেদ করে। QM বৃত্তটির ব্যাস হলে, প্রমাণ করো যে, /_QPR=2/_RQM. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
যদি বিচ্যুতি di=(ξ−22), 22= কাল্পনিক গড়, ∑f=500 এবং ∑fi=100 হয়, তাহলে যৌগিক গড ¯x এর মান—
View Solutionদুই বন্ধু যথাক্রমে 40,000 টাকা ও 50,000 টাকা দিয়ে একটি যৌথ ব্যাবসা শুরু করেন । তাদের মধ্যে চুক্তি হয় যে, লাভের 50% নিজেদের মধ্যে সমান ভাগে এবং লাভের অবশিষ্টাংশ মূলধনের অনুপাতে ভাগ হবে । প্রথম বন্ধুর লভ্যাংশের পরিমাণ যদি দ্বিতীয় বন্ধুর লভ্যাংশ অপেক্ষা 800 টাকা কম হয়, তবে প্রথম বন্ধুর লভ্যাংশের পরিমাণ নির্ণয় করো ।
View SolutionIf (p2+q2),(pq+qr),(q2+r2) are in GP then prove that p, q, r are in GP.
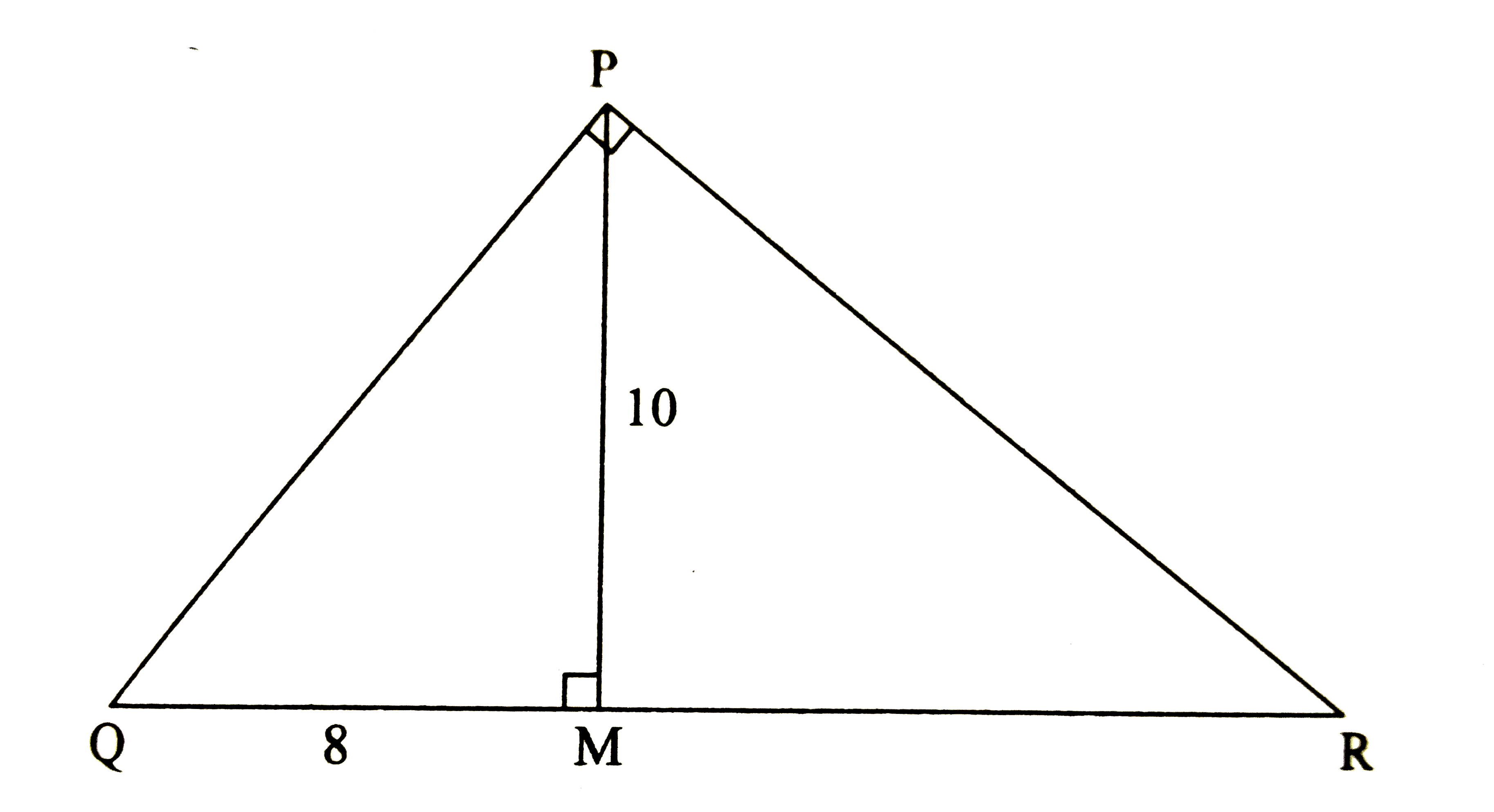
View SolutionIn the figure, ∠QPR=90∘, seg PM⊥ seg QR and Q−M−R, PM=10. QM=8, find QR.
View SolutionQR is a chord of the circle with centre O. Two tangents drawn at eh points Q and R intersect each other at the point P. If QM is a diameter, prove that ∠QPR=2∠RQM[GP−X]
View SolutionTwo circles intersect each other at P externally. The straight QR touches the circle at two points Q and R. Prove that ∠QPR=1 right angle.
View Solutionकिसी वृत के केंद्र O पर उसकी एक जीवा OQ,130∘ का कौन बनाती है | Q और R पर की स्पर्शरेखाऐं बिंदु P पर मिलती है ∠QPR की माप निकालें |
View Solutionf(x)=x2−1x−1অপেক্ষকেরলেখচিত্রঅঙ্কনকরােএবংx = 1ওx= 2 বিন্দুতে অপেক্ষক সন্তত কি না তা লেখচিত্র থেকে বলাে।
View Solutionএকটি অপেক্ষক f(x)-এর নিম্নরূপ সংজ্ঞা দেওয়া হয় । f(x)={(x−1","যখন x>0),(−12","যখনx=0),(x+1","যখনx<0):}f(x)অপেক্ষকেরলেখচিত্রঅঙ্কনকরাে।লেখচিত্রথেকেf(x)অপেক্ষকেরx =-1/2বিন্দুতেমাননির্ণয়করােএবংx = 0বিন্দুতেf(x) সন্তত কি না বলে।
View Solution6 সেমি ব্যাসার্ধবিশিষ্ট বৃত্তে কোনো চাপ 20∘17′সম্মুখ।কোণউৎপন্নকরে।৪ সেমি ব্যাসার্ধবিশিষ্ট বৃত্তে ওই চাপ যে পরিমাণ সম্মুখ কোণ উৎপন্ন করে তার ষষ্টিক পরিমাপ নির্ণয় করো।
View Solution[θ=srঅথবা কণ (বৃত্তীয় মানে )=(চাপ)/(ব্যাসার্ধ),সূত্র−সম্পর্কিতপেশ্নাবলি।]দুটিবৃত্তএমনযে,একটিঅপরটিকেন্দ্রবিন্দুগামী।প্রথমবৃত্তেরlদৈর্ঘ্যেরচাপতারকেন্দ্রেthetaএবংদ্বিতীয়বৃত্তেরmদৈর্ঘ্যেরচাপতারকেন্দ্রেphiসম্মুখকোণউৎপন্নকরে।প্রমাণকরােযে,lphi=mtheta।
View Solutionযদি |z1|=|z2|এবংarg z1 + arg z2 = 0হয়,তবেপ্রমাণকরোz1 = 1/(z2)।
View Solutionযদি |z1|=|z2|এবংarg z1 ~ arg z2 = piহয়,তবেপ্রমাণকরোz1 + z2 = 0।
View Solutionমনে করো xy সমতলে অবস্থিত S একটি বৃত্ত, যা x2+y2 = 4 সমীকরণ দ্বারা সংজ্ঞাত। মনে করো S বৃত্তের ওপর P এমন একটি বিন্দু যার স্থানাঙ্ক দুটি (x স্থানাঙ্ক ও yস্থানাঙ্ক) ধনাত্মক। মনে করো P বিন্দুতে S বৃত্তের স্পর্শক অক্ষদ্বয়কে M ও N বিন্দুতে ছেদ করেছে। তবে MN সরলরেখার মধ্যবিন্দু যে বক্রের ওপর অবস্থিত, তা হল—
View Solutionপ্রতিটি প্রশ্নে বিবৃতি-1 এবং বিবৃতি-2 দেওয়া আছে। প্রতিটি প্রশ্নের বিবৃতি দুটি নীচের কোন বিকল্পটিকে (A, B, C ও D-এর মধ্যে) সঠিকভাবে ব্যাখ্যা করে? সরলরেখা l:→r=ˆi−ˆj+ˆk+t(2ˆi+3ˆj−6ˆk) এবং সমতল p:→r.(2ˆi+3ˆj−6ˆk)=7। বিবৃতি−1সরলরেখাlসমতলp−কেএকটিঅনন্য(unique)বিন্দুতেছেদকরে।বিবৃতি−2l সরলরেখা p সমতলের ওপর লম্ব।
View SolutionUsing the properties of determinants show that : ∣∣ ∣ ∣∣⎡⎢⎣p2q2r2qrrppqpqr⎤⎥⎦∣∣ ∣ ∣∣=(p−q)(q−r)(r−p)(pq+qr+rp)
View Solution
