A Δ B=………Solution in Telugu
(A−B)∪(B−A)
(A∩B)−(B∩A)
both A & B
A-B
Step by step video & image solution for A Delta B=……… by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Which of the following are sets? Justify your answer.
The collection of all even integers.
View SolutionThe decimal expansion of 2714 is
View SolutionIn △ABC, DE∣∣BC and AD=13BD.
If BC = 4.5cm, Find DE.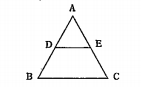
View SolutionIn a triangle ABC,r1+r21+cosC is equal to 2abcDelta (b) (a+b)cDelta abc2Delta (d) abcDelta2
View SolutionA=[[1,23,4]],B=[[5,67,8]], Prove that Delta(A)dot Delta(B)=Delta(AB)
View SolutionThe triangle with vertices (a,b),(a,a),(b,a) is
View Solutionif Δ=∣∣ ∣∣−xabb−xaab−x∣∣ ∣∣ then a factor of Δ is
View SolutionIf Δ=∣∣ ∣∣−xabb−xaab−x∣∣ ∣∣ then a factor of Δ is -
View SolutionIf Z=A4B13CD32 ,than relative error in Z ΔZZ is equal to
(a) (ΔAA)4+(ΔBB)13−(ΔCC)−(ΔDD)32
(b) 4(ΔAA)+(13)(ΔBB)+(ΔCC)+(32)(ΔDD)
(c) 4(ΔAA)+13(ΔBB)−(ΔCC)−(32)(ΔDD)
(d) (ΔAA)4+13(ΔBB)+(ΔCC)+32(ΔDD)
View SolutionSuppose A, B and C are three sets such that AΔB=ϕ, then AΔ(BΔC) is equal to
View Solutionif Δ=∣∣ ∣∣−xabb−xaab−x∣∣ ∣∣ then a factor of Δ is
View SolutionIf the medians of a △ABC intersect at G, show that ar(△AGB)=ar(△AGC)=ar(△BGC)=13ar(△ABC). GIVEN : △ABC such that its medians AD,BE and CF intersect at G. TO PROVE : ar(△AGB)=ar(△BGC)=ar(△AGC)=13ar(△ABC)
View SolutionIf the medians of a △ABC intersect at G, show that ar(△AGB)=ar(△AGC)=ar(△BGC)=13ar(△ABC). GIVEN : △ABC such that its medians AD,BE and CF intersect at G TO PROVE : ar(△AGB)=ar(△BGC)=ar(△CGA)=13ar(△ABC).
View SolutionIf the measured values of two quantities are A±ΔA and B±ΔB, and ΔA and ΔB being the mean absolute errors. What is the maximum possible error in A+B? Show that if Z=AB then ΔZZ=ΔAA+ΔBB
View Solution(A) : If am.bnCP.dq, then the percentages error in the measurement of x, Δxx=m(Δaa)+n(Δbb)+p(Δcc)+q(Δdd)
(R) : The above is true for all values of Δa,Δb,ΔcandΔb.
View SolutionProve theAΔ(BΔC)=(AΔB)ΔC
View Solution
