If the angle of depression from a lighthouse of two ships situated in the same line with the lighthouse are 60∘ and 30∘ and if the nearer ship is 150 in away from the lighthouse, then find the distance of the other ship from the lighthouse.Solution in Bengali
Step by step video & image solution for If the angle of depression from a lighthouse of two ships situated in the same line with the lighthouse are 60^@ and 30^@ and if the nearer ship is 150 in away from the lighthouse, then find the distance of the other ship from the lighthouse. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Choose the correct option in each case from the following questions : In a partnership business, the ratio of share of profit of two friends is 1/2 : 1/3, then the ratio of their principal is ____
View SolutionChoose the correct option in each case from the following questions : Interest on ₨. A at the simple interest 10% per annum for b months is ____
View SolutionAs observed from the top of a 75m tall lighthouse, the angles of depression of two ships are 30o and 45o . If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
View SolutionFrom a top of a lighthouse, an observer looks at the ship and find the angle of depression to be 45∘. If the height of the lighthouse is 1000m, then how far is that ship from the lighthouse.
View SolutionThe angle of depression of a ship as observed from the top of a lighthouse is 45∘ . If the height of the lighthouse is 200 m , then what is the distance of the ship from the foot of the lighthouse ?
View SolutionFrom the top of a lighthouse , an observer looks at a ship and finds the angle of depression to be 30∘. If the height of the lighthouse is 100m, then find how far is that ship from the lighthouse.
View SolutionA ship of height 24 m is sighted from a lighthouse. From the top of the lighthouse the angle of depression to the top of the mast and base of the ship is 30∘and45∘ respectively. How far is the ship from the lighthouse ? (√3=1.73)
View Solutionएक प्रकाश स्तम्भ को ऊँचाई 40 मीटर है। प्रकाश स्तम्भ के शीर्ष से एक जहाज का अवनमन कोण 60∘ है। प्रकाश स्तम्म का जहाज से दूरी ज्ञात कीजिए।
View SolutionAs observed from the top of a 75m high lighthouse from the sea-level, the angles of depression of two ships are 30∘ and 45∘ . If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
View SolutionTwo ships are sailling in the sea on the two sides of a lighthouse. If the distance between the ships is 10(√3+1) meters and their angle of elevations of the top of the lighthouse are 60∘and45∘, then the height of the lighthouse is (The two ships and the foot of lighthouse are in a straight line)
View Solution60 मीटर ऊँचे प्रकाश स्तम्भ की चोटी से एक जहाज का अवनमन कोण 60 है तो प्रकाश स्तम्भ पद से जहाज की दूरी ज्ञात कीजिए।
View SolutionThe angles of depression of two ships from the top of a lighthouse are 45∘and30∘. If the ships are 120 m apart, then find the height of the lighthouse.
View SolutionAs observed from the top of a 75m high lighthouse from the sea-level, the angles of depression of two ships are 30∘and45∘. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships
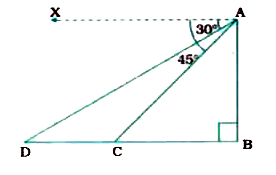
View SolutionThe angle of depression of a ship as observed from the top of a lighthouse is 45∘ . If the height of the lighthouse is 200 m , then what is the distance of the ship from the foot of the lighthouse ?
View SolutionA ship of height 24 m is sighted from a lighthouse. From the top of the lighthouse the angle of depression to the top of the mast and base of the ship is 30∘and45∘ respectively. How far is the ship from the lighthouse ? (√3=1.73)
View SolutionFrom the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 30∘. If the height of the lighthouse is 100 m, then find how far is that ship from the lighthouse.
View Solution
