The mean of a frequency distribution is 8.1, if fixi = 132 + 5K and fi = 20 then what is the value of K?Solution in Bengali
Step by step video & image solution for The mean of a frequency distribution is 8.1, if fixi = 132 + 5K and fi = 20 then what is the value of K? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A sum of money at simple interest amounts to ₹ 815 in 3years and to ₹ 854 in 4years. The sum is
View SolutionThe population of a village increase by r% each year. If P be the population after n years, then population n years ago was
View SolutionIf the mean of a frequency distribution is 8.1 and ∑fixi=132+5k, ∑fi=20 , then k= (a) 3 (b) 4 (c) 5 (d) 6
View Solutionयदि निम्नलिखित बारंबारता बंटन का माध्य 20 है, तो p का मान ज्ञात कीजिए :

View Solutionयदि निम्नलिखित बारम्बारता बंटन का माध्य 20 है, तो p का मान ज्ञात कीजिए :

View SolutionThe arithmitic mean of a frequency distraction is 8. If Σfixi=130+5k and Σfi=20, then find the value of k.
View Solutionयदि एक बारम्बारता बंटन का माध्य 8.1 है तथा ∑fixi=132+5k,∑fi=20, है , तो k=
View SolutionIf the mean of the following frequency distribution is 7.2 find value of 'K'.
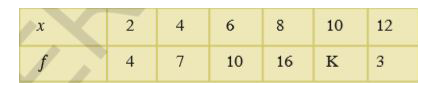
View SolutionIf the mean of the following frequency distribution is 7.2 find value of 'K'.
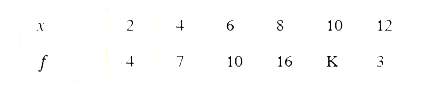
View SolutionIf the mean of the following frequency distribution is 7.2 find value of 'K'.
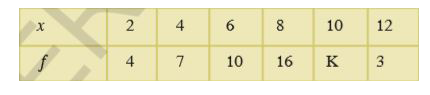
View SolutionIf the mean of the following frequency distribution is 7.2 find value of 'K'.

View SolutionIf the mean of a frequency distribution is 8.1 and ∑fixi=132+5k, ∑fi=20 , then k= (a) 3 (b) 4 (c) 5 (d) 6
View SolutionIf the mean of the following frequency distribution is 50 , then find the value of k.

View SolutionThe mean of a frequency distribution is 8.1, if fixi = 132 + 5K and fi = 20 then what is the value of K?
View SolutionIf the mean of a frequency distribution is 8.1 ∑fixi=133+5k and ∑fi=30, find the value of k.
View SolutionIf the mean of a frequency distribution is 8.1 and ∑fixi=132+5K,∑fi=20 then K =
View Solution
