Two tangetns from A and B which are lie on the circle intersect at the point P. If ∠APB=68∘ then find the measurement of ∠PAB.Solution in Bengali
Step by step video & image solution for Two tangetns from A and B which are lie on the circle intersect at the point P. If angleAPB = 68^@ then find the measurement of anglePAB. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If the total intetest in 5 yeas is 15 the of its principal, then rate of interest per annum is
View SolutionIf the total interest of some money in y years at the rate of simple interest x% per annum is Rs Pyx25, then the principal becomes
View Solutionकिसी O केंद्र वाले वृत्त पर स्तिथ दो बिन्दुओ A तथा B से खींची गई स्पर्श रेखाए P पर प्रतिछेदित करती है, यदि चतुर्भुज ,PAOB में, ∠AOB:∠APB=5:1 तब ∠APB ज्ञात करे?
View Solutionदो वृत्तों के केन्द्र O और O ' है, जो एक-दूसरे को बाहृतः बिन्दु P पर स्पर्श करते है। इन वृत्तों की एक उभयनिष्ट अनुस्पर्श रेखा AB खींची जाती है। सिद्ध कीजिए कि ∠APB=90∘.
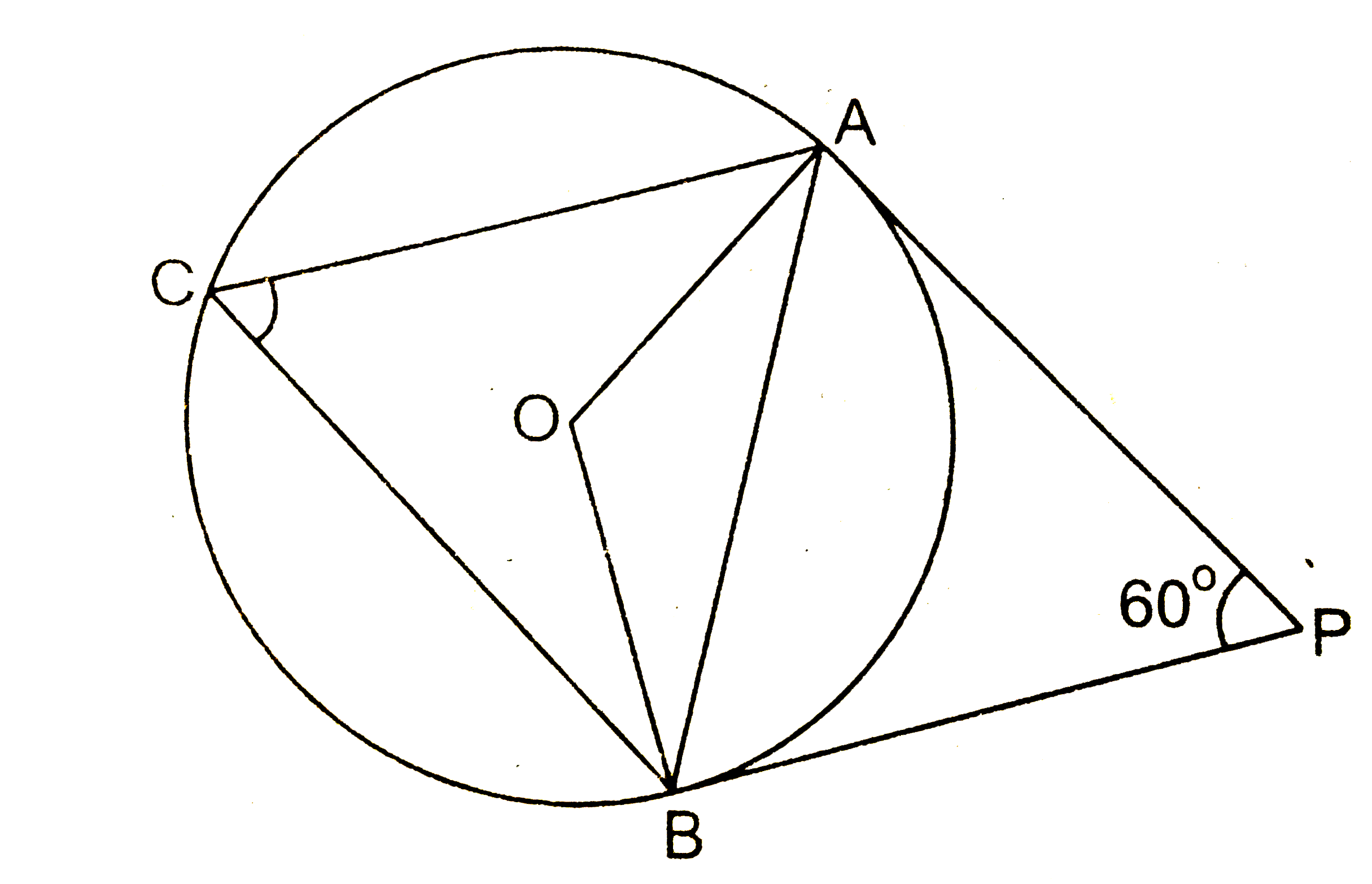
View SolutionTwo tangents drawn at the point A and B on a circle intersect each other at the point P. If ∠APB=60∘, then ∠PAB=
View SolutionTwo tangents are drawn from a point P to a circle at A and B. O is the centre of the circle. If ∠AOP=60∘, then ∠APB is
View SolutionA (a,0) , B (-a,0) are two points . If a point P moves such that ∠PAB−∠PBA=π/2 then find the locus of P.
View SolutionA(a,0) , B(-a,0) are two point . If a point P moves such that ∠PAB−∠PBA=2α then find the locus of P .
View SolutionIf two circles intersect at point P and a simple line ABCD intersects the outer circle at A and D and the inner circle at B and C, prove that angleAPB=angleCPD|
View Solutionचित्र में, वृत्त ABC जिसका केन्द्र O हैं, पर किसी बाह्रा बिन्दु से खींची गई स्पर्श रेखाएँ PA और PB वृत्त को बिन्दु A तथा B पर स्पर्श करती हैं। यदि ∠APB=60∘ हो तो
(i) ∠AOB,(ii)∠ACB की माप ज्ञात कीजिए।
View SolutionTwo circles intersects in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that the A,Q,B and T lie on a circle.
View SolutionTwo diagonals AC and BD of a cyclic quadrilateral ABCD intersect at P. If ∠APB=68∘ and ∠CBD=24∘, then ∠ADB =
View SolutionTwo circles touch externally at P. A direct common tangent AB to two circles touch the circles at A and B. Then the measure of ∠APB is
View SolutionThe tangents at two points A and B on the circle with the centre O intersects at P, if in quadrilateral ∠AOB:∠APB=5:1, then the measure of ∠APB is____
View SolutionTwo tangents to a circle at A and B intersect at a point P. If ∠APB=68∘ then find ∠PAB.
View Solution
