A circle with center in the first quadrant is tangent to y=x+10,y=x−6, and the y−axis. Let (h,k) be the center of the circle. If the value of (h+k)=a+b√a where √a is a surd, find the value of a+b.
Step by step video & image solution for A circle with center in the first quadrant is tangent to y = x+10, y = x - 6, and the y- a x is. Let (h, k) be the center of the circle. If the value of (h + k) = a + b sqrta where sqrta is a surd, find the value of a +b. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A circle with center in the first quadrant is tangent to y=x+10,y=x-6 and the Y-axis. Let (p,q) be the centre of the circle. If the value oif (p+q)=a+b√a when a, b∈Q, then the value of |a-b| is
View SolutionThe sides of a triangle ABC lie on the lines 3x+4y=0,4x+3y=0 and x=3 . Let (h,k) be the centre of the circle inscribed in △ABC. The value of (h+k) equals
View Solution
Knowledge Check
A circle is tangent to the lines with the equations x = 5 and y = 7. Which of the following could be the coordinates of the center of the circle ?
A(3, 7)B(8, 4)C(10, 8)D(10, 14)A circle with center (5,-2) is tangent to the y-axis. What is the equation of the circle ?
A(x−5)2+(y+2)2=25Bx2+y2=25C(x+5)2+(y−2)2=25Dx2+y2=5If the tangent the curve y2+3x−7=0 at the point (h,k) is parallel to the line x - y = 4 , then the value of k is
A−23B−32C32D23
Find the area enclosed between first quadrant of a circle x2+y2=16 and line y=x.
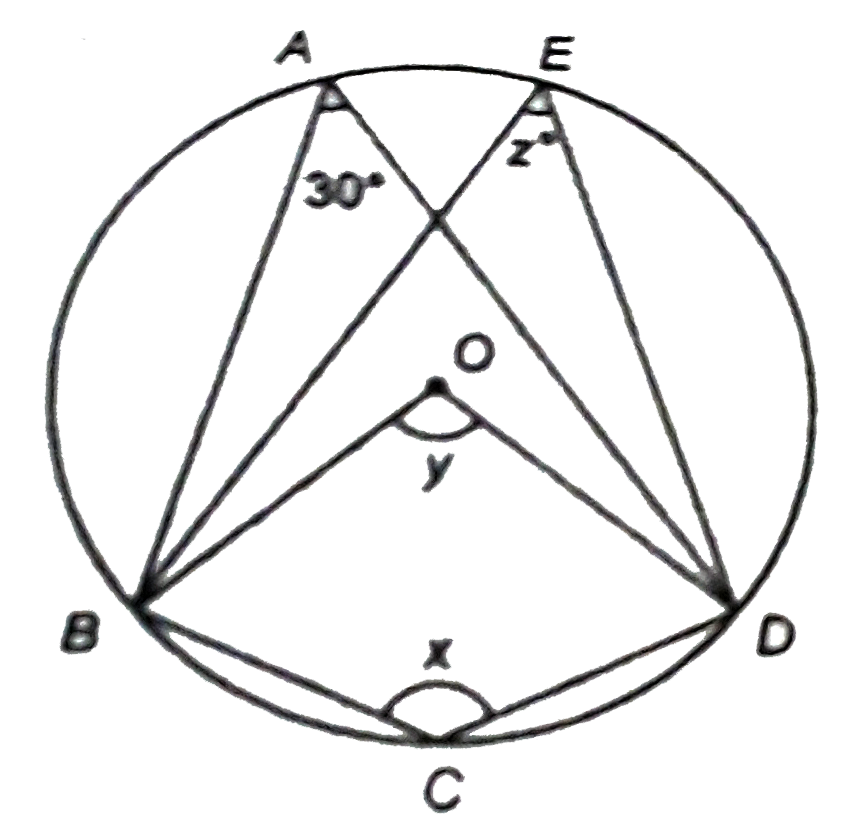
View SolutionIn the adjoining figure , O is the center of the circle. If ∠BAD=30∘ , then find the values of x,y and z.
View SolutionThe line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the center of the circle lies on x−2y=4 . Then find the radius of the circle.
View SolutionArea of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
View Solution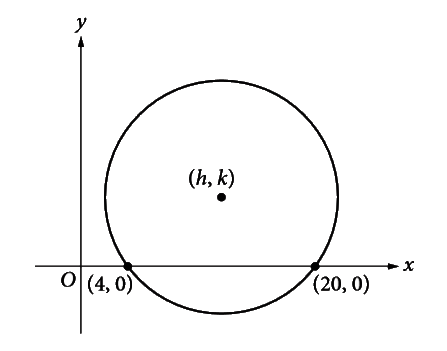
In the xy-plane above, the circle has center (h, k) and radius 10. What is the value of k ?
View Solution
