18 points are indicated on the perimeter of a triangle ABC (see figure). If three points are choosen probability it will form a triangle. Figure 331816 (b) 12 (c) 355408 (d) 711816
To solve the problem of finding the probability that three points chosen from 18 points on the perimeter of triangle ABC will form a triangle, we can follow these steps:
Step 1: Understand the total points
We have 18 points on the perimeter of triangle ABC, which includes 3 vertices (A, B, C) and 15 other points distributed along the sides.
Step 2: Calculate total ways to choose 3 points
The total number of ways to choose 3 points from 18 is given by the combination formula:
Total ways=(183)
Calculating this:
(183)=18×17×163×2×1=816
Step 3: Identify collinear points
Next, we need to identify the points that cannot form a triangle. The points on each side of the triangle are collinear. Since there are 5 points on each side (excluding the vertices), we have:
- Side AB: 5 points
- Side BC: 5 points
- Side CA: 5 points
Thus, there are a total of 15 collinear points (5 points on each of the 3 sides).
Step 4: Calculate ways to choose 3 collinear points
The number of ways to choose 3 points from these collinear points on each side is:
Collinear ways=3×(53)
Calculating (53):
(53)=5×42×1=10
Thus, the total number of ways to choose 3 collinear points is:
Collinear ways=3×10=30
Step 5: Calculate valid triangles
Now, we can find the number of valid triangles that can be formed by subtracting the collinear combinations from the total combinations:
Valid triangles=(183)−Collinear ways=816−30=786
Step 6: Calculate the probability
Finally, the probability that three randomly chosen points will form a triangle is given by:
Probability=Valid trianglesTotal ways=786816
This fraction can be simplified:
786816=131136
Step 7: Final answer
The final answer for the probability that three points chosen will form a triangle is:
711816
We have 18 points on the perimeter of triangle ABC, which includes 3 vertices (A, B, C) and 15 other points distributed along the sides.
The total number of ways to choose 3 points from 18 is given by the combination formula:
Total ways=(183)
Calculating this:
(183)=18×17×163×2×1=816
Next, we need to identify the points that cannot form a triangle. The points on each side of the triangle are collinear. Since there are 5 points on each side (excluding the vertices), we have:
- Side AB: 5 points
- Side BC: 5 points
- Side CA: 5 points
The number of ways to choose 3 points from these collinear points on each side is:
Collinear ways=3×(53)
Calculating (53):
(53)=5×42×1=10
Thus, the total number of ways to choose 3 collinear points is:
Collinear ways=3×10=30
Now, we can find the number of valid triangles that can be formed by subtracting the collinear combinations from the total combinations:
Valid triangles=(183)−Collinear ways=816−30=786
Finally, the probability that three randomly chosen points will form a triangle is given by:
Probability=Valid trianglesTotal ways=786816
This fraction can be simplified:
786816=131136
The final answer for the probability that three points chosen will form a triangle is:
711816
Topper's Solved these Questions
Similar Questions
18 points are indicated on the perimeter of a triangle ABC . If three points are choosen probability it will form a triangle. 331816 (b) 12 (c) 355408 (d) 711816
View Solution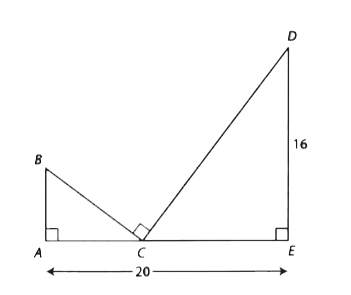
What is the area of triangle ABC (see figure above)?
(1) DC=20
(2) AC=8.
View SolutionWrite the perimeter of the triangle formed by the points O(0, 0), A(a, 0) and B(0, b) .
View SolutionFind the orthocentre of the triangle ABC whose angular points are A(1,2),B(2,3)andC(4,3)
View SolutionTriangle ABC (see figure) has a base of 2y, a height of y, and an area of 49. What is y?
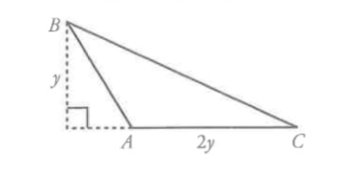
View SolutionGiven two points A and B. If area of triangle ABC is constant then locus of point C in space is
View SolutionIf D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD=12AC
View SolutionThe coordinates of the centriod of triangle ABC where A,B,C are the points of intersection of the plane 6x+3y−2z=18 with the coordinate axes are :
View SolutionFind the area of a triangle formed by the points A(5, 2), B(4, 7) and C(7,4).
View SolutionD is a point on the side BC of a triangle ABC such that ∠ADC=∠BAC. Show that CA2=CB.CD.
View Solution
