AB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3AB and C Is the midpoint of AB. If AC and CB subtend angles $α$ and $β$ , respectively, at P, then the value of tan $β$ is

Video Solution

Answer

Step by step video & image solution for AB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3AB and C Is the midpoint of AB. If AC and CB subtend angles alpha and beta, respectively, at P, then the value of tanbeta is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

BOOK - RESONANCE DPP ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions
15videos
INVERSE TRIGONOMETRIC FUNCTIONS
BOOK - RESONANCE DPP ENGLISHCHAPTER - MATRICESEXERCISE - All Questions
7videos
MATRICES

Knowledge Check

Question 1 - Select One

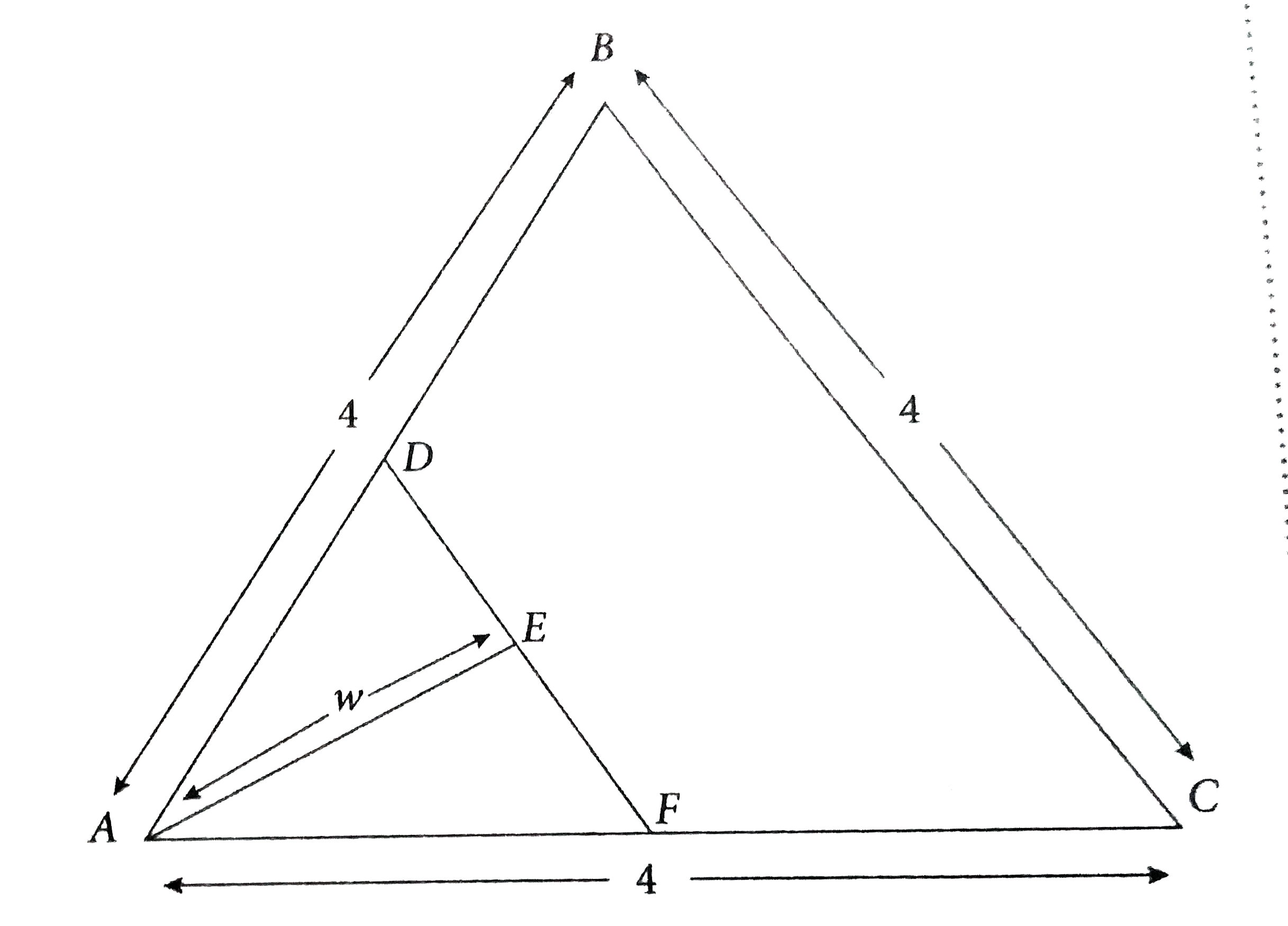
$Δ A B C$ is equilateral and $∠ A E F$ is a right angle . D and F are the midpoints of AB and AC, respectively. What is the value of w?
A1
B $\sqrt{3}$
C2
D $2 \sqrt{3}$

AB is vertical tower. The point A is on the ground and C is the middle point of AB. The part CB subtend an angle $α$ at a point P on the ground. If $A P = n A B$ , then $tan α =$
View Solution
If $\to a$ & $\to b$ are the position vectors of $A$ & $B$ respectively and $C$ is a point on $A B$ produced such that $A C = 3 A B$ then the position vector of $C$ is:
View Solution
If the coordinates of midpoints of $A B and A C o f Δ$ A B C are (3,5) and (-3,-3) respectively, then write the length of side BC.
View Solution
If A=(2, -3, 7), B = (-1, 4, -5) and P is a point
on the line AB such that $A P : B P = 3 : 2$ then P
has the coordinates
View Solution
At the point of intersection of the curves $y^{2} = 4 a x and x y = c^{2}$ , the tangents to the two curves make angles $α and β$ respectively with x-axis. Then $tan α cot β =$
View Solution
Let a vertical tower $A B$ have its end $A$ on the level ground. Let $C$ be the mid point of $A B$ and $P$ be a point on the ground such that $A P = 2 A B .$ If $∠ B P C = β,$ then $tan β$ is equal to : (1) $\frac{2}{9}$ (2) $\frac{4}{9}$ (3) $\frac{6}{7}$ (4) $\frac{1}{4}$
View Solution
The angles of elevation of a cliff at a point A on the ground and at a point B 100 mt vertically above A are $α$ are $β$ respectively.The height of the cliff in metres is
View Solution

RESONANCE DPP ENGLISH-JEE MAINS-All Questions

A fair coin is tossed repeatedly. If tail appears on first four tosses...
01:17
If int(x+1)/(x^2+x+3)dx=a ln|x^2+x+3|+1/(sqrt(b))tan^(-1)((c x+d)/(sqr...
04:24
AB is a vertical pole resting at the end A on the level ground. P is ...
02:28
A bird is sitting on the top of a vertical pole 20 m high and its elev...
02:02
Evaluate int(-1)^(3)("tan"^(-1)x/(x^(2)+1)+"tan"^(-1)(x^(2)+1)/x)dx.
03:07
If In=intsin^n xdxn in N , t h e n5I4-6I6 is equal to s in x(cosx)^5+...
04:51
int0^pisin^3theta(1+2costheta)(1+costheta)^2dtheta is equal to 1/3 (...
04:53
If AD, BE and CF are the medians of a DeltaA B C ,t h e n(A D^2+B E^2+...
04:44
The value of int(-(pi/4)^(1/3))^((pi/4)^(1/3))(x^2)/((1+sin^2x^3)(1+e^...
12:52
If H is the orthocentre of a triangle ABC, then the radii of the cir...
08:31
I(1)=int(0)^((pi)/2)Ln (sinx)dx, I(2)=int(-pi//4)^(pi//4)Ln(sinx+cosx)...
08:37
Find the coordinates of a point on the parabola y=x^2+7x+2 which is cl...
04:12
Let (d)/(dx )F(x) =((e ^(sin x ))/(x )), x gt 0 If int(1 )^(4) (3)/(x)...
02:42
If in Delta ABC, (a -b) (s-c) = (b -c) (s-a), prove that r(1), r(2), r...
03:18
Show that int0^(pi/2)sqrt((sin2theta))sintheta d theta=pi/4
08:27
If in triangle ABC (r)/(r(1))=(1)/(2), then the value of tan(A/2)(tan(...
06:39
Let u=int0^1("ln"(x+1))/(x^2+1)dx a n d v=int0^(pi/2)ln(sin2x)dx ,t h ...
07:41
A golf ball is dropped from a height of 80 m. Each time the ball hi...
02:36
if |f(x1)-f(x2)|<=(x1-x2)^2Find the equation of tangent to the curve y...
02:38
From the point (lambda,3) tangents are drawn to x^(2)/9+y^(2)/4=1 and ...
04:13

Home
Ask Doubt
Profile

AB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3AB and C Is the midpoint of AB. If AC and CB subtend angles α and β, respectively, at P, then the value of tanβ is

Topper's Solved these Questions

Similar Questions

Knowledge Check

ΔABC is equilateral and ∠AEF is a right angle . D and F are the midpoints of AB and AC, respectively. What is the value of w?

RESONANCE DPP ENGLISH-JEE MAINS-All Questions

AB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3AB and C Is the midpoint of AB. If AC and CB subtend angles $α$ and $β$ , respectively, at P, then the value of tan $β$ is

$Δ A B C$ is equilateral and $∠ A E F$ is a right angle . D and F are the midpoints of AB and AC, respectively. What is the value of w?