A person has to buy 4 ice creams. Number of ways he can choose 4 ice creams from 10 different ice-cream shops (given every shop has sufficient number of ice creams and all ice creams are of same type) (1)9C4 (2) 13C4 (3) 9C3 (4) 10C4
To solve the problem of how many ways a person can choose 4 ice creams from 10 different ice cream shops, we can use the concept of combinations. Here’s the step-by-step solution:
Step 1: Understand the Problem
We need to choose 4 ice creams from 10 different shops. Each shop has an unlimited supply of ice creams, and all ice creams are of the same type.
Step 2: Identify the Variables
- Let n be the total number of ice cream shops, which is 10.
- Let r be the number of ice creams to choose, which is 4.
Step 3: Use the Combinations Formula
The number of ways to choose r items from n items is given by the formula for combinations:
nCr=n!r!(n−r)!
In our case, we need to calculate 10C4.
Step 4: Calculate 10C4
Substituting the values into the formula:
10C4=10!4!(10−4)!=10!4!⋅6!
Now we can simplify this:
10C4=10×9×8×74×3×2×1
Calculating the numerator:
10×9=90
90×8=720
720×7=5040
Now calculating the denominator:
4×3=12
12×2=24
24×1=24
Now divide the numerator by the denominator:
10C4=504024=210
Step 5: Conclusion
The number of ways the person can choose 4 ice creams from 10 different shops is 10C4.
Final Answer
Thus, the correct option is (4) 10C4.
---
We need to choose 4 ice creams from 10 different shops. Each shop has an unlimited supply of ice creams, and all ice creams are of the same type.
- Let n be the total number of ice cream shops, which is 10.
- Let r be the number of ice creams to choose, which is 4.
The number of ways to choose r items from n items is given by the formula for combinations:
nCr=n!r!(n−r)!
In our case, we need to calculate 10C4.
Substituting the values into the formula:
10C4=10!4!(10−4)!=10!4!⋅6!
Now we can simplify this:
10C4=10×9×8×74×3×2×1
Calculating the numerator:
10×9=90
90×8=720
720×7=5040
Now calculating the denominator:
4×3=12
12×2=24
24×1=24
Now divide the numerator by the denominator:
10C4=504024=210
The number of ways the person can choose 4 ice creams from 10 different shops is 10C4.
Thus, the correct option is (4) 10C4.
Topper's Solved these Questions
Similar Questions
Explain, why-one feels ice cream at 0∘C colder than water at 0∘C ?
View SolutionIn a shop there are five types of ice-creams available. A child buys six ice-creams. Statement -1: The number of different ways the child can buy the six ice-creams is ^10C5 . Statement -2: The number of different ways the child can buy the six ice-creams is equal to the number of different ways of arranging 6 As and 4 Bs in a row.
View SolutionIn a shop there are five types of ice-creams available. A child buys six ice-creams. Statement -1: The number of different ways the child can buy the six ice-creams is ^10C5 . Statement -2: The number of different ways the child can buy the six ice-creams is equal to the number of different ways of arranging 6 As and 4 Bs in a row.
View SolutionIn a shop, there are five types of ice-creams available. A child buys six ice-creams.
Statement-1: The number of different ways the child can buy the six ice-creams is .10C4.
Statement-2: The number of different ways the child can buy six ice-creams is equal to the number of different ways to arranging 6A's and 4B's in a row.
View SolutionArun bought 14 kg of ice cream. After his children had eaten some, there was 110 kg left. How much did his children eat?
View SolutionA rectangular block of ice measures 40cm by 25cm by 15cm. Calculate its weight in kg, if ice weighs 910 of the weight of the same volume of water and 1 cm3 of water weighs 1 gm.
View SolutionThe total number of ways of selecting 4 letters from the word NARAYANA is: (A) 10 (B) 9 (C) 12 (D) none of these
View SolutionA group of 123 workers went to a canteen for cold drinks, ice-cream and tea, 42 workers took ice-cream, 36 tea and 30 cold drinks. 15 workers purchased ice-cream and tea, 10 ice-cream and cold drinks, and 4 cold drinks and tea but not ice-cream, 11 took ice-cream and tea but not cold drinks. Determine how many workers did not purchase anything?
View SolutionWhich one of the following is an example of a cube?
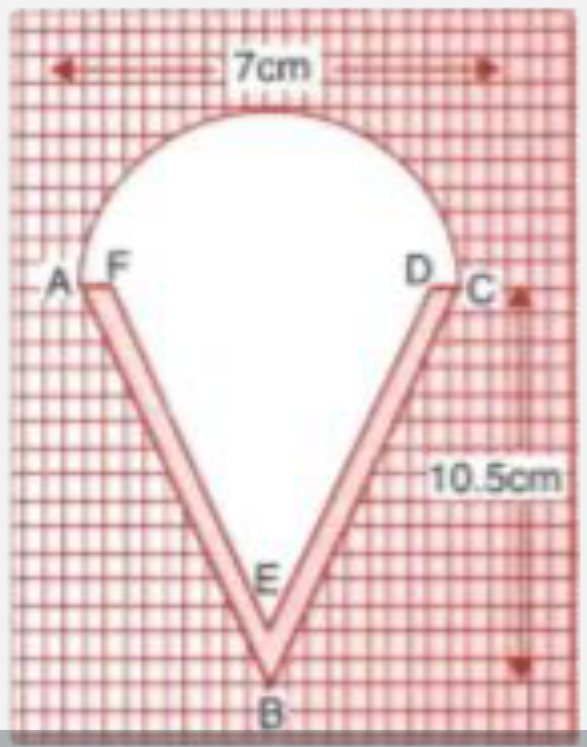
View SolutionThe given figure shows the cross-section of an ice cream cone consisting of a cone surmounted by a hemisphere. The radius of the hemisphere is 3.5 cm and the height of the cone is 10-5 cm. The outer shell ABCDEF is shaded and is not filled with ice-cream. AF = DC = 0.5 cm, AB // FE and BC // ED. Calculate :
(i) the volume of the ice-cream in the cone (the internal volume of the cone including the hemisphere) in cm3,
(ii) the volume of the outer shell (the shaded portion) in cm3.
In each case, give your answer correct to the nearest cm3.
View Solution
