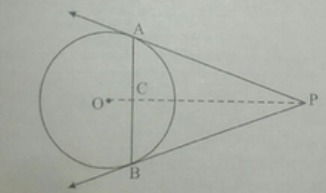
Tangents PA and PB are drawn to the circle x2+y2=4,then locus of the point P if PAB is an equilateral triangle ,is equal to
To find the locus of the point P such that the tangents PA and PB drawn to the circle x2+y2=4 form an equilateral triangle PAB, we can follow these steps:
Step 1: Understand the Circle
The given circle is x2+y2=4. This circle has its center at the origin (0, 0) and a radius of 2.
Step 2: Identify Points A and B
Let P be a point from which tangents PA and PB are drawn to the circle. The points A and B are the points of tangency on the circle.
Step 3: Use the Property of Concyclic Points
Since PAB is an equilateral triangle, the points P, A, B, and O (the center of the circle) are concyclic. This means they lie on the same circle.
Step 4: Determine the Diameter
For the points P, A, B, and O to be concyclic, the line segment OP must be the diameter of the circle that passes through points A and B.
Step 5: Equation of the Circle
Let P be represented by coordinates (x1,y1). The equation of the circle with diameter OP can be derived using the formula for the circle through two points (the endpoints of the diameter):
(x−x1)(x+0)+(y−y1)(y+0)=0
This simplifies to:
x2+y2−x1x−y1y=0
Step 6: Final Equation
Thus, the locus of point P is given by the equation:
x2+y2−x1x−y1y=0
This represents the locus of point P as it moves around the circle.
Summary
The locus of the point P, from which tangents PA and PB are drawn to the circle x2+y2=4 such that PAB forms an equilateral triangle, is given by the equation:
x2+y2−x1x−y1y=0
The given circle is x2+y2=4. This circle has its center at the origin (0, 0) and a radius of 2.
Let P be a point from which tangents PA and PB are drawn to the circle. The points A and B are the points of tangency on the circle.
Since PAB is an equilateral triangle, the points P, A, B, and O (the center of the circle) are concyclic. This means they lie on the same circle.
For the points P, A, B, and O to be concyclic, the line segment OP must be the diameter of the circle that passes through points A and B.
Let P be represented by coordinates (x1,y1). The equation of the circle with diameter OP can be derived using the formula for the circle through two points (the endpoints of the diameter):
Thus, the locus of point P is given by the equation:
The locus of the point P, from which tangents PA and PB are drawn to the circle x2+y2=4 such that PAB forms an equilateral triangle, is given by the equation:
Topper's Solved these Questions
Similar Questions
From point P(4,0) tangents PA and PB are drawn to the circle S:x2+y2=4. If point Q lies on the circle, then maximum area of △QAB is- (1) 2√3 (2) 3√3 (3) 4√3 A) 9
View SolutionTangents PA and PB are drawn to x2+y2=4 from the point P(3,0). Area of triangle PAB is equal to:-
View SolutionIf tangents PA and PB are drawn from P(−1,2) to y2=4x then
View SolutionTangents PA and PB are drawn to the circle (x−4)2+(y−5)2=4 from the point P on the curvey=sinx , where A and B lie on the circle. Consider the function y=f(x) represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?
View SolutionFrom the point P(3, 4) tangents PA and PB are drawn to the circle x2+y2+4x+6y−12=0. The area of Δ PAB in square units, is
View SolutionTangents PAandPB are drawn to the circle x2+y2=8 from any arbitrary point P on the line x+y=4. The locus of mid-point of chord of contact AB is
View SolutionFrom a point P perpendicular tangents PQ and PR are drawn to ellipse x2+4y2=4, then locus of circumcentre of triangle PQR is
View SolutionTangents PT1,andPT2, are drawn from a point P to the circle x2+y2=a2. If the point P lies on the line Px+qy+r=0, then the locus of the centre of circumcircle of the triangle PT1T2 is
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O and radius r. If OP=2r, show that △APB is equilateral.

View SolutionFrom an external point P, two tangents PA and PB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
View Solution
