There are 50 machines in a factory each producing 1000 bolts daily. For each additional machine installed, the output per machine drops by 10 bolts. How many additional machines should be installed to maximize the total output per day? 20 (b) 30 (c) 50 (d) 25
To solve the problem of maximizing the total output of bolts produced by the machines in the factory, we can follow these steps:
Step 1: Define the Variables
Let x be the number of additional machines installed. Initially, there are 50 machines, and each machine produces 1000 bolts daily.
Step 2: Determine the Output per Machine
For each additional machine installed, the output per machine decreases by 10 bolts. Therefore, the output per machine when x additional machines are installed is:
Output per machine=1000−10x
Step 3: Calculate the Total Number of Machines
The total number of machines after installing x additional machines is:
Total machines=50+x
Step 4: Calculate the Total Output
The total output O per day can be expressed as:
O=(Total machines)×(Output per machine)=(50+x)(1000−10x)
Expanding this, we get:
O=(50+x)(1000−10x)=50000−500x+1000x−10x2=50000+500x−10x2
This simplifies to:
O=−10x2+500x+50000
Step 5: Identify the Quadratic Function
The total output O is a quadratic function of the form:
O=−10x2+500x+50000
This is a downward-opening parabola, which means it has a maximum point.
Step 6: Find the Vertex of the Parabola
The vertex of a quadratic function ax2+bx+c occurs at x=−b2a. Here, a=−10 and b=500:
x=−5002×−10=50020=25
Conclusion
To maximize the total output, the number of additional machines that should be installed is:
25
Let x be the number of additional machines installed. Initially, there are 50 machines, and each machine produces 1000 bolts daily.
For each additional machine installed, the output per machine decreases by 10 bolts. Therefore, the output per machine when x additional machines are installed is:
Output per machine=1000−10x
The total number of machines after installing x additional machines is:
Total machines=50+x
The total output O per day can be expressed as:
O=(Total machines)×(Output per machine)=(50+x)(1000−10x)
Expanding this, we get:
O=(50+x)(1000−10x)=50000−500x+1000x−10x2=50000+500x−10x2
This simplifies to:
O=−10x2+500x+50000
The total output O is a quadratic function of the form:
O=−10x2+500x+50000
This is a downward-opening parabola, which means it has a maximum point.
The vertex of a quadratic function ax2+bx+c occurs at x=−b2a. Here, a=−10 and b=500:
x=−5002×−10=50020=25
To maximize the total output, the number of additional machines that should be installed is:
25
Topper's Solved these Questions
Similar Questions
The total cost of producing x radio sets per day is Rs.x2435x+25 and the price per set at which they may be sold is Rs.50−x2. Find the daily output to maximize the total profit.
View SolutionA manufacturer produces nuts and bolts. It takes 2 hours work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 2 hours on machine B to produce a package of bolts. He earns a profit of Rs. 24 per package on nuts and Rs. 18 per package on bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates his machines for at the most 10 hours a day. Make an L.P.P. from above and solve it graphically ?
View Solution
Knowledge Check
Twelve identical machines, running continuously at the same constant rate, take 8 days to complete a shipment. How many additional machines, each running at the same constant rate, would be needed to reduce the time required to complete a shipment by 2 days?
A2B3C4D6
A mill owner buys two types of machines A and B for his mill, Machines A occupies 1,000 sq.m of area and requires 12 men to operate it, while machine B occupies 1,200 sq.m of area and requires 8 men to operate it. The owner has 7,600 sq.m of area available and 72 men to operate the machines. If machine A produces 50 units and machine B produces 40 units daily, how many machines of each type should he buy to maximize the daily output? Use Linear Programming to find the solution.
View SolutionA factory owner purchases two types of machines, A and B, for his factory. The requirements and limitations for the machines are as follows:

He has an area of 7600 sq. m available and 72 skilled men who can operate the machines. To find how many machines of each type should he buy to maximize the daily output, formulate this as a L.P.P.
View SolutionA manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs 17.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machine for at most 12 hours a day?
View SolutionRaghu has enough money to buy 75 machines worth Rs.200 each. How many machines can he buy if he gets a discount of Rs.50 on each machine ?
View SolutionA factory has three machines X, Y, and Z producing 1000, 2000 and 3000 bolts per day respectively. the machine X produces 1% defective bolts, Y produces 1.5% and Z produces 2% defective bolts. At the end of a day, a bolt is drawn at random and is found to be defective. What is the probability that this defective bolt has been produced by machine X?
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:
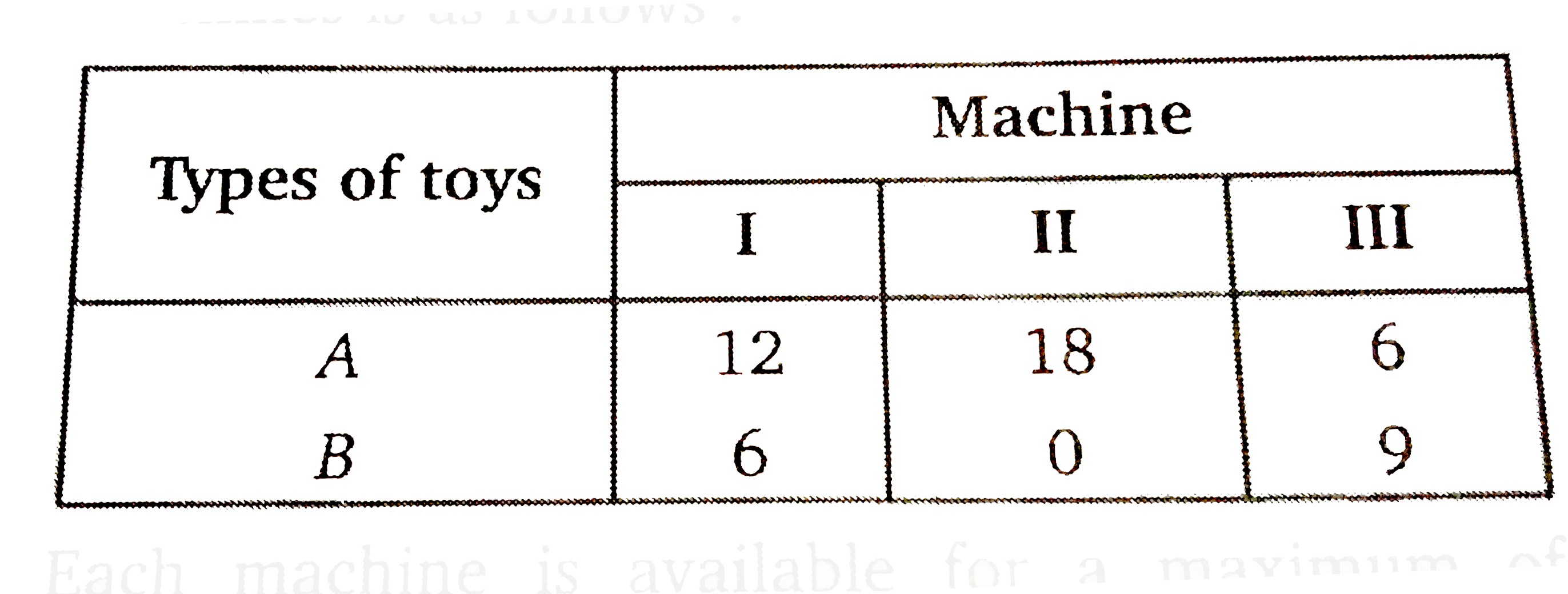 Each machine is available for a
maximum of 6 hours per day. If the profit
Each machine is available for a
maximum of 6 hours per day. If the profit
View SolutionA company manufactures two types of toys A and B. A toy of type A requires 5 minute for cutting and 10 minute for assembling. A toy of type B requires 8 minute for cutting and 8 minutes for assembling. There are 3 hours available for cutting and 4 hours available for assembling th etoys in a day. The profit is Rs 50 each on a toy of Type A and Rs 60 each on a toy of type B. How many toys of each type should the company manufacture in a day to maximize the profit ? Use linear programming to find the solution.
View Solution
