Find number of digits in 1820
To find the number of digits in 1820, we can use the formula for the number of digits d in a number n, which is given by:
d=⌊log10n⌋+1
Step 1: Define the number
Let n=1820.
Step 2: Take the logarithm
We will take the logarithm (base 10) of both sides:
log10n=log10(1820)
Using the logarithmic identity log10(ab)=b⋅log10a, we can rewrite this as:
log10n=20⋅log1018
Step 3: Simplify log1018
Next, we can express 18 in terms of its prime factors:
18=2⋅32
Using the property of logarithms that states log10(a⋅b)=log10a+log10b, we have:
log1018=log10(2⋅32)=log102+log10(32)=log102+2⋅log103
Step 4: Substitute known values
Using known values for logarithms:
- log102≈0.301
- log103≈0.477
Substituting these values, we get:
log1018=0.301+2⋅0.477=0.301+0.954=1.255
Step 5: Calculate log10n
Now we can substitute log1018 back into our equation for log10n:
log10n=20⋅1.255=25.1
Step 6: Find the number of digits
Now we can find the number of digits d:
d=⌊log10n⌋+1=⌊25.1⌋+1=25+1=26
Thus, the number of digits in 1820 is 26.
Summary
The number of digits in 1820 is 26.
Let n=1820.
We will take the logarithm (base 10) of both sides:
Next, we can express 18 in terms of its prime factors:
Using known values for logarithms:
- log103≈0.477
Now we can substitute log1018 back into our equation for log10n:
Now we can find the number of digits d:
The number of digits in 1820 is 26.
Topper's Solved these Questions
Similar Questions
If log2=0.30101, log3=0.47712, then the number of digits in 620 is 15 b. 16 c. 17 d. 18
View SolutionIn the figure as shown find the number of digits in the length of AB.
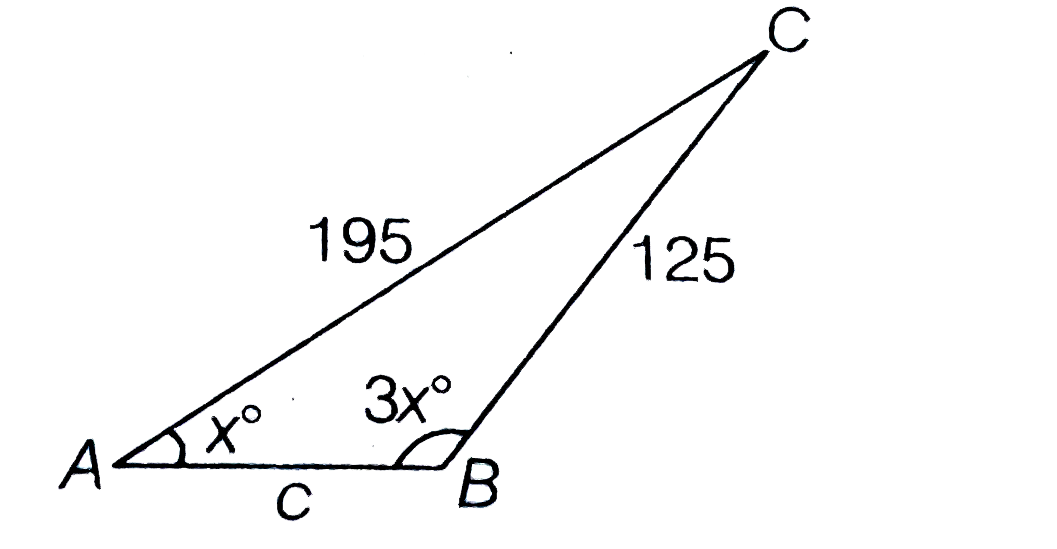
View SolutionFind the number of digits 525
View SolutionFind number of four-digit numbers in which repetition is not allowed. Also find number of four-digit numbers in which at least one digit is repeated.
View SolutionFind the number of n digit numbers, which contain the digits 2 and 7, but not the digits 0, 1, 8, 9.
View SolutionFind the number of n digit numbers, which contain the digits 2 and 7, but not the digits 0, 1, 8, 9.
View SolutionFind the number of all 6-digit natural numbers having exactly three odd digits and three even digits.
View SolutionFind the number of 5 digit numbers with different digits having middle term greatest and with non-zero digits?
View SolutionFind the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5 if no digit is repeated. How many of these will be even?
View SolutionFind the numbers of 4-digit numbers that can be formed using the digits, 1,2,3,4,5 if no digit is repeated ? How many of these will be even?
View Solution
