A ship is fitted with three engines . The engines function independently of each other with respective probabilities . For the ship to be operational at least two of its engines must function. Let denote the event that the ship is operational and let denote, respectively, the events that the engines are function. Which of the following is/are true? (a) (b)(exactly two engines of the ship are functioning ) (c) (d)
Step by step video & image solution for A ship is fitted with three engines E_1,E_2 and E_3. The engines function independently of each other with respective probabilities 1/2, 1/4, and 1/4. For the ship to be operational at least two of its engines must function. Let X denote the event that the ship is operational and let X_1, X_2 and X_3 denote, respectively, the events that the engines E_1, E_2 and E_3 are function. Which of the following is/are true? (a) P(X_1^c "|"X)=3/(16) (b)P(exactly two engines of the ship are functioning "|"X ) =7/8 (c) P(X"|"X_2)=5/6 (d) P(X"|"X_1)=7/(16) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the range of the following functions:
f(x)=ex1+|x|,x≥0 [.] denotes the greatest integer function.
View SolutionE and F are two independent events. The probability that both e and F happen is 1/12 and the probability that neither E nor F happens is 1/2. Then
View SolutionStatement -1 : Let E1,E2,E3 be three events such that P(E1)+P(E2)+P(E3)=1, then E1,E2,E3 are exhaustive events.
Statement-2 if the events E1,E2 and E3 be exhaustive events, then P(E1∪E2∪E3)=1
View SolutionDifferentiate the following function tan−1(ex) with respect to x
View SolutionSuppose E1,E2andE3 be three mutually exclusive events such that P(Ei)=pi for i=1,2,3.
P(none of E1,E2,E3) equals
View SolutionLet E=(1,2,3,4)andF−(1,2). Then the number of onto functions from E to F is:
View SolutionFind the value of ∫1−1[x2+{x}]dx,where[.]and{.} denote the greatest function and fractional parts of x, respectively.
View SolutionThe letters of the word PRABABILITY are written down at random in a row. Let E1 denotes the event that two Is are together and E2 denotes the event that B's are together, then P(E1)=P(E2=311 (b) P(E1∩E2)=255 P(E1∪E2)=1855 (d) P(E1E2)=15
View SolutionSuppose E1,E2andE3 be three mutually exclusive events such that P(Ei)=pi for i=1,2,3.
If p1,p2andp3 are the roots of 27x3−27x2+ax−1=0 the value of a is
View SolutionSuppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E1)=12andP(E1∣E2)=14. Observe the lists given below :
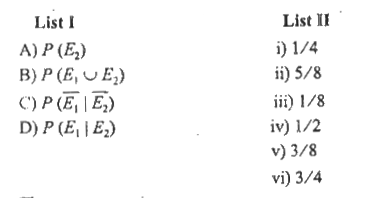
The correct matching of the list I from the list II is :
View Solution
