Let f(x)=∫x−2e(1+t)2dt and g(x)=f(h(x)),where h(x) is defined for all x∈R. If g'(2)=e4 and h'(2)=1 then absolute value of sum of all possible values of h(2), is ___
Step by step video & image solution for Let f(x) =int_(-2)^xe^((1+t)^2)dt and g(x) = f(h(x)),where h(x) is defined for all x in R. If g'(2) = e^4 and h'(2)=1 then absolute value of sum of all possible values of h(2), is ___ by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Let f(x)=√x2−4x and g(x) = 3x . The sum of all values for which f(x) = g(x) is
A−8.5B0C8D9.4
Let f(x)=−1+|x−2|andg(x)=1−|x| then set of all possible value (s) of for which (fog) (x) is discontinuous is:
View SolutionLet f(x)=[x],g(x)=|x|andf{g(x)}=h(x) ,where [.] is the greatest integer function . Then h(-1) is
View SolutionLet f(x)=∫x2dt√1+t4andg be the inverse of f. Then, the value of g'(0) is
View SolutionGraph of y=f(x)andy=g(x) is given in the following figure. If h(x)=f(g(x)), then find the value of h'(2).
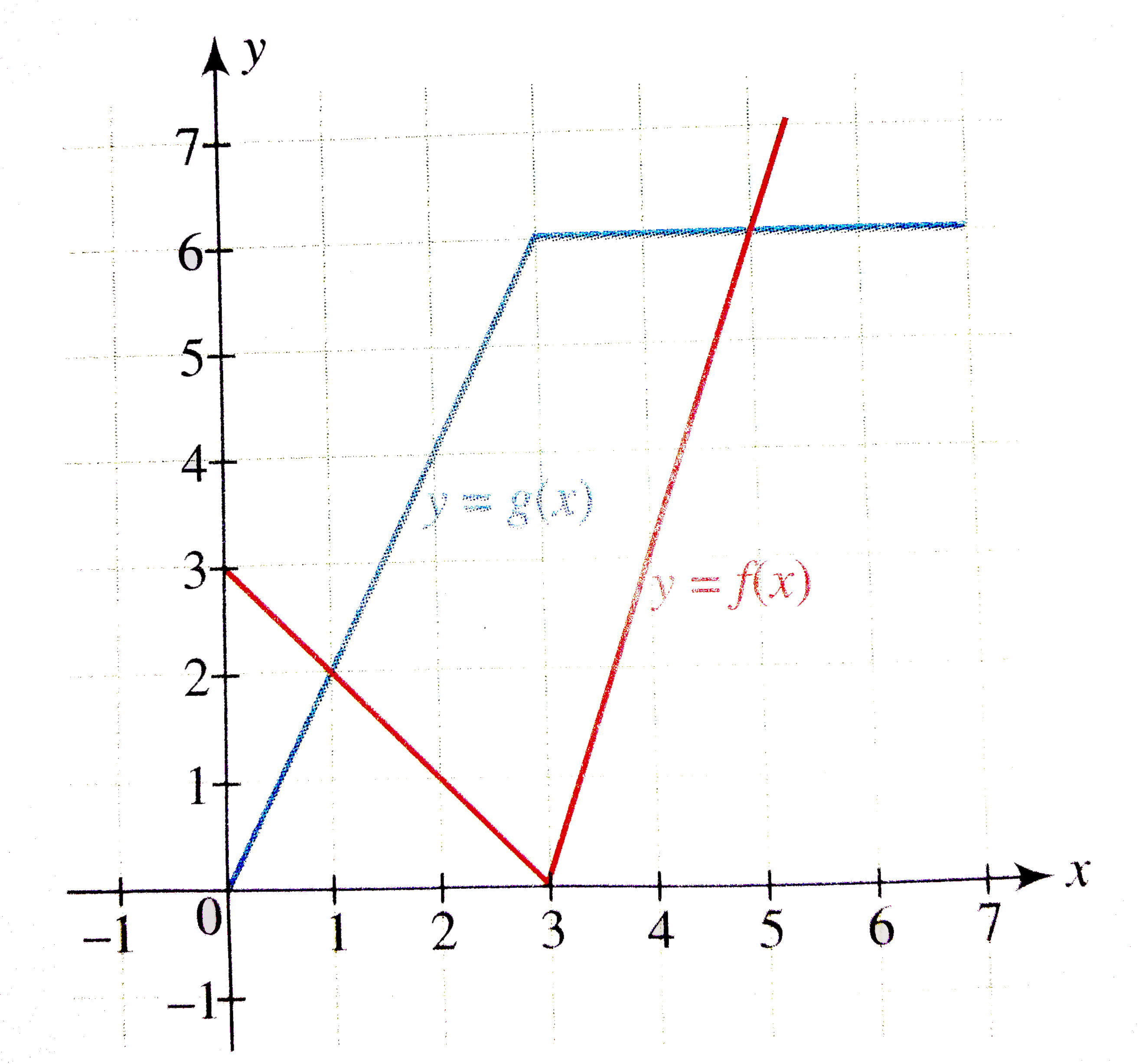
View SolutionLet f(x)=∫x0dt√1+t3 and g(x) be the inverse of f(x). Then the value of 4g''(x)g(x)2 is________.
View SolutionLet f be a differentiable function such that f(1) = 2 and f'(x) = f (x) for all x∈R. If h(x)=f(f(x)), then h'(1) is equal to
View SolutionLet f(x)=ex−xandg(x)=x2−x,∀x∈R. Then, the set of all x∈R, when the function h(x)=(fog)(x) is increasing, in
View Solution
