Prove that x3p+x3q+1+x3r+2 is exactly divisible by x2+x+1, if p,q,r is integer.
To prove that x3p+x3q+1+x3r+2 is exactly divisible by x2+x+1, we can follow these steps:
Step 1: Identify the roots of x2+x+1
The roots of the polynomial x2+x+1 can be found using the quadratic formula:
x=−b±√b2−4ac2a
Here, a=1,b=1,c=1:
x=−1±√12−4⋅1⋅12⋅1=−1±√−32=−1±√3i2
Let ω=−1+√3i2 and ω2=−1−√3i2.
Step 2: Substitute ω into the polynomial
We need to evaluate f(ω)=ω3p+ω3q+1+ω3r+2.
Step 3: Simplify using properties of ω
Since ω3=1, we can simplify the powers:
ω3p=(ω3)p=1p=1
ω3q=(ω3)q=1q=1andω3q+1=ω3q⋅ω=1⋅ω=ω
ω3r=(ω3)r=1r=1andω3r+2=ω3r⋅ω2=1⋅ω2=ω2
Step 4: Combine the results
Now substituting these values into f(ω):
f(ω)=1+ω+ω2
Step 5: Use the identity for roots of unity
From the property of roots of unity, we know that:
1+ω+ω2=0
Thus, we have:
f(ω)=0
Step 6: Repeat for ω2
Now we evaluate f(ω2):
f(ω2)=(ω2)3p+(ω2)3q+1+(ω2)3r+2
Using similar simplifications:
(ω2)3p=1,(ω2)3q=1,(ω2)3q+1=ω2,(ω2)3r=1,(ω2)3r+2=ω
Thus:
f(ω2)=1+ω2+ω=0
Conclusion
Since f(ω)=0 and f(ω2)=0, by the Factor Theorem, f(x)=x3p+x3q+1+x3r+2 is divisible by x2+x+1.
Therefore, we conclude that x3p+x3q+1+x3r+2 is exactly divisible by x2+x+1.
---
The roots of the polynomial x2+x+1 can be found using the quadratic formula:
x=−b±√b2−4ac2a
Here, a=1,b=1,c=1:
x=−1±√12−4⋅1⋅12⋅1=−1±√−32=−1±√3i2
Let ω=−1+√3i2 and ω2=−1−√3i2.
We need to evaluate f(ω)=ω3p+ω3q+1+ω3r+2.
Since ω3=1, we can simplify the powers:
ω3p=(ω3)p=1p=1
ω3q=(ω3)q=1q=1andω3q+1=ω3q⋅ω=1⋅ω=ω
ω3r=(ω3)r=1r=1andω3r+2=ω3r⋅ω2=1⋅ω2=ω2
Now substituting these values into f(ω):
f(ω)=1+ω+ω2
From the property of roots of unity, we know that:
1+ω+ω2=0
Thus, we have:
f(ω)=0
Now we evaluate f(ω2):
f(ω2)=(ω2)3p+(ω2)3q+1+(ω2)3r+2
Using similar simplifications:
(ω2)3p=1,(ω2)3q=1,(ω2)3q+1=ω2,(ω2)3r=1,(ω2)3r+2=ω
Thus:
f(ω2)=1+ω2+ω=0
Since f(ω)=0 and f(ω2)=0, by the Factor Theorem, f(x)=x3p+x3q+1+x3r+2 is divisible by x2+x+1.
Similar Questions
Knowledge Check
In Figure 1, y=√3xandz=2x. What is the ratio p:q:r in figure 2?
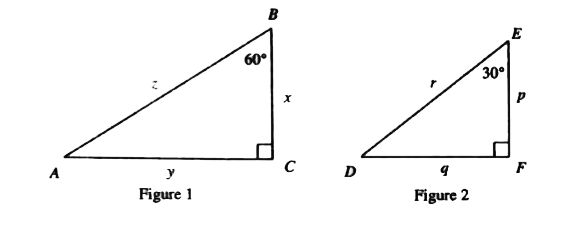 A1:2:3B√3:1:2C1:√3/2:1D2:√3:1
A1:2:3B√3:1:2C1:√3/2:1D2:√3:1
Let P(x) and Q(x) be two polynomials.Suppose that f(x)=P(x3)+xQ(x3) is divisible by x2+x+1, then (a) P(x) is divisible by (x-1),but Q(x) is not divisible by x -1 (b) Q(x) is divisible by (x-1), but P(x) is not divisible by x-1 (c) Both P(x) and Q(x) are divisible by x-1 (d) f(x) is divisible by x-1
View SolutionFind the values of p and q so that x4+px3+2x2−3x+q is divisible by (x2−1)
View SolutionThe polynomial px3+4x2−3x+q completely divisible by x2−1: find the values of p and q. Also for these values of p and q factorize the given polynomial completely.
View Solution
Statement-1: The coefficient of a3b4c3 in the expansion of (a−b+c)10 is 10!3!4!3!
Statement-2: The coefficient of xpyqzr in the expansion of (x+y+z)n is n!p!q!r! for all integer n.
View SolutionProve that pxq−r+qxr−p+rxp−q>p+q+r,wherep,q,r are distinct and x≠1.
View SolutionIf p(x)=x5+4x4−3x2+1 andg(x)=x2+2, then divide p(x) by g(x) and find quotient q(x) and remainder r(x).
View SolutionGiven that q2−pr,0, p>0, then the value of |pqpx+qyqrqx+rypx+qyqx+ry0| is- a. zero b. positive c. negative d. q2+pr
View Solution
