If the cube roots of unity are 1,ω,ω2, then the roots of the equation (x−1)3+8=0 are a. −1,1+2ω,1+2ω2 b. −1,1−2ω,1−2ω2 c. −1,−1,−1 d. none of these
Step by step video & image solution for If the cube roots of unity are 1,omega,omega^2, then the roots of the equation (x-1)^3+8=0 are a. -1,1+2omega,1+2omega^2 b. -1,1-2omega,1-2omega^2 c. -1,-1,-1 d. none of these by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
if 1,ω,ω2 root of the unity then The roots of the equation (x−1)3+8=0 are
View SolutionIf 3√−1=−1,−ω,−ω2 , then roots of the equation (x+1)3+64=0 are
View SolutionIf ω is a cube root of unity, then
1+ω2= …..
View SolutionIf ω is a cube root of unity, then
1+ω= …..
View SolutionIf 1,ω,ω2 are the cube roots of unity, then △
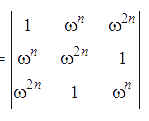
is equal to.....
View SolutionIf ω is a complex cube root of unity, then a root of the equation
∣∣ ∣ ∣∣x+1ωω2ωx+ω21ω21x+ω∣∣ ∣ ∣∣=0, is
View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
(1−ω)(1−ω2)=3
View SolutionIf 1,ω,ω2 be three roots of 1, show that: (1−ω+ω2)2+(1+ω−ω2)2=−4
View SolutionIf ω is a cube root of unity and △=∣∣∣12ωωω2∣∣∣, then △2 is equal to (A) −ω (B) ω (C) 1 (D) ω2
View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
(1−ω−ω2)6=64
View Solution
