If A=[ab−ba],B=[−ab−b−a] then find A+B
To find the sum of the matrices A and B, we will follow these steps:
1. Identify the matrices:
A=[ab−ba],B=[−ab−b−a]
2. Set up the addition:
We need to add the matrices A and B:
A+B=[ab−ba]+[−ab−b−a]
3. Add corresponding elements:
We will add the corresponding elements of the matrices:
- First row, first column: a+(−a)=a−a=0
- First row, second column: b+b=2b
- Second row, first column: −b+(−b)=−b−b=−2b
- Second row, second column: a+(−a)=a−a=0
Thus, we can write:
A+B=[02b−2b0]
4. Final result:
The sum of the matrices A and B is:
A+B=[02b−2b0]
A=[ab−ba],B=[−ab−b−a]
We need to add the matrices A and B:
A+B=[ab−ba]+[−ab−b−a]
We will add the corresponding elements of the matrices:
- First row, first column: a+(−a)=a−a=0
- First row, second column: b+b=2b
- Second row, first column: −b+(−b)=−b−b=−2b
- Second row, second column: a+(−a)=a−a=0
A+B=[02b−2b0]
The sum of the matrices A and B is:
A+B=[02b−2b0]
Similar Questions
If A=[1−12−1] and B=[a1b−1] and (A+B)2=A2+B2, then find the value of a and b.
View SolutionLet A=⎡⎢⎣abcbcacab⎤⎥⎦ then find tranpose of A matrix
View SolutionFind the values of a and b if A=B, where A=[a+43b8−6],B=[2a+2b2+28b2−5b]
View SolutionIf A={a,b} and B={3}, find A×B
View SolutionIf A×B={(a,x),(a,y),(b,x),(b,y)}, then find A and B
View Solution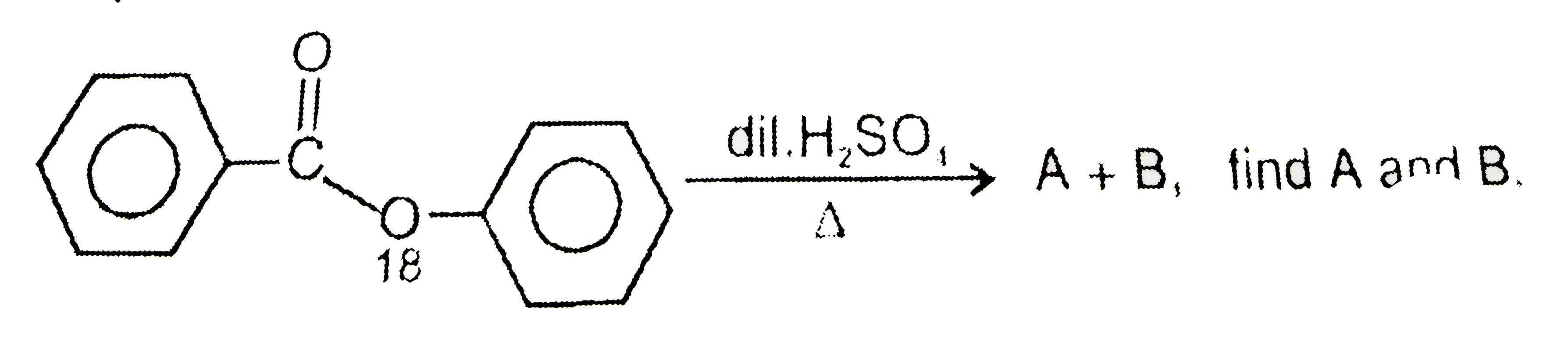
A+B, Find A and B
View SolutionIf sets A=[−4,1]andB=[0,3), then find the following sets:
(a) A∩B (b) A∪B (c ) A−B
(d) B−A (e ) (A∪B)' (f) (A∩B)'
View SolutionIf A=[1−12−1],B=[a−1b−1] and (A+B)2=(A2+B2) then find the values of a and b.
View SolutionIf sin(A-B) = 12 and cos(A+B) = 12, 0o < A+B <90o and A>B, then find A and B.
View SolutionThree vertices of a parallelogram are (a+b, a−b), (2a+b, 2a−b), (a−b, a+b) . Find the fourth vertex.
View Solution