There are 6 items in column A and 6 items in column B. A student is asked to match each item in column A with an item in column B. How many possible, correct or incorrect, answer are there to this question?
To solve the problem of matching 6 items in column A with 6 items in column B, we need to determine the total number of possible arrangements (or matches) between the two columns.
1. Understanding the Problem: We have 6 items in column A and 6 items in column B. Each item in column A can be matched with any item in column B.
2. Total Matches Calculation: The first item in column A can be matched with any of the 6 items in column B. After matching the first item, the second item in column A can be matched with any of the remaining 5 items in column B, and so on.
3. Using Factorials: The total number of ways to arrange or match the items can be calculated using the factorial notation. The total number of arrangements (matches) can be expressed as:
6!=6×5×4×3×2×1
4. Calculating Factorial: Now we calculate 6!:
6!=720
5. Conclusion: Therefore, the total number of possible matches (correct or incorrect) between the items in column A and column B is 720.
Final Answer:
The total number of possible matches is 720.
6!=6×5×4×3×2×1
6!=720
The total number of possible matches is 720.
Similar Questions
Match item in column A with those given in column B.
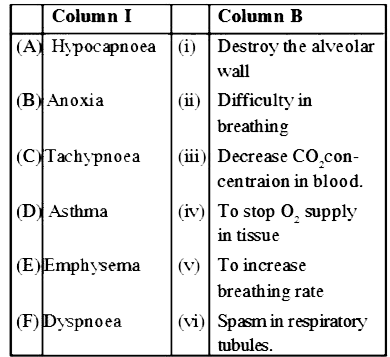
View SolutionMatch the items in column A with those in Column B :

View SolutionMatch the items in column 'A' with those in column 'B'

View SolutionMatch the items in Column A with those in Column B.
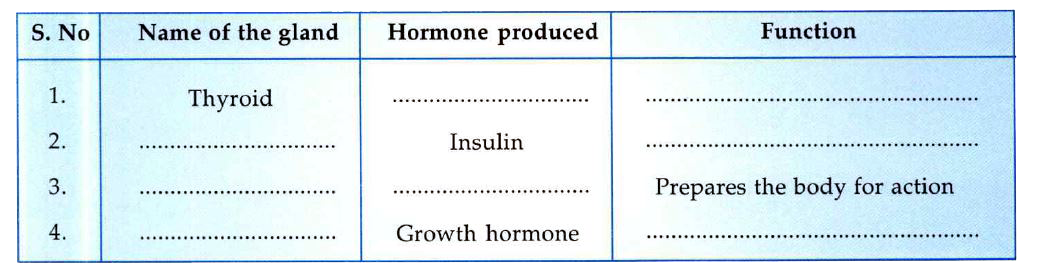
View SolutionMatch the items in column I with relevant items in column II

View SolutionMatch the items in Column I with those in Column II
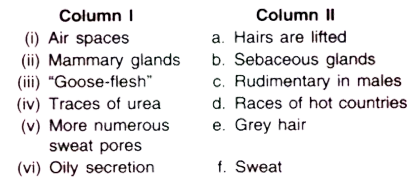
View SolutionMatch the items in Column with those in Column II.

View SolutionMatch items in Column I with those in Column II:
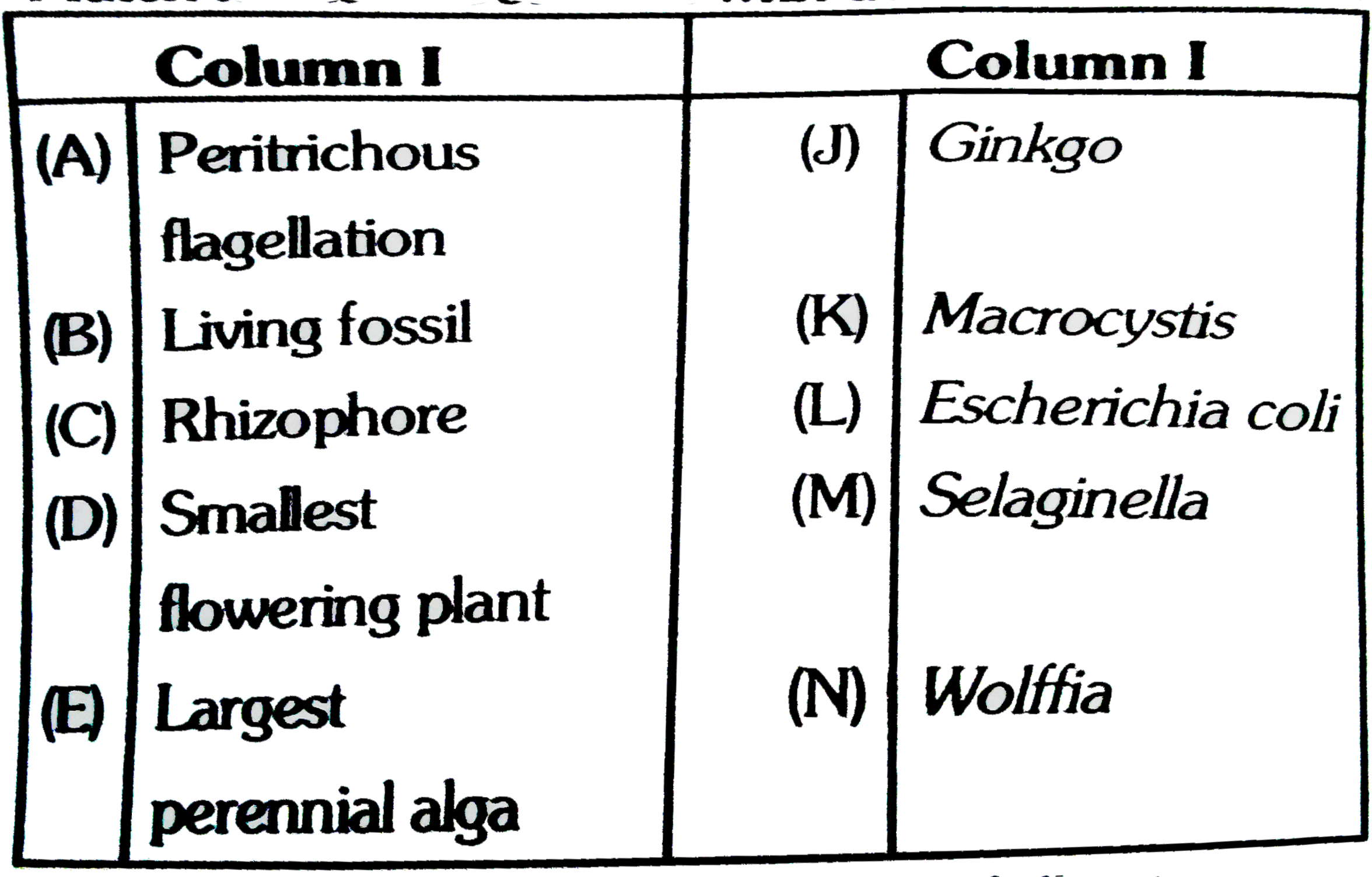
View SolutionMatch the items in column I with those given in column II.
View SolutionMatch the items of Column I with items of Column II.

View Solution
