Find the single arithmetic mean between: (a−b)and(a+b)
To find the single arithmetic mean between (a−b) and (a+b), we can follow these steps:
Step 1: Identify the two numbers
The two numbers given are:
- First number: a−b
- Second number: a+b
Step 2: Let the arithmetic mean be X
We denote the arithmetic mean by X. In an arithmetic progression (AP), the mean is the middle term, so we have:
- a−b,X,a+b
Step 3: Set up the equation for common difference
In an AP, the common difference between consecutive terms is constant. Therefore, we can express the common difference D in two ways:
1. From the first term to the mean:
D=X−(a−b)
2. From the mean to the second term:
D=(a+b)−X
Step 4: Equate the two expressions for D
Since both expressions represent the same common difference, we can set them equal to each other:
X−(a−b)=(a+b)−X
Step 5: Simplify the equation
Now, we simplify the equation:
X−a+b=a+b−X
Adding X to both sides gives:
2X−a+b=a+b
Now, subtract b from both sides:
2X−a=a
Step 6: Solve for X
Now, we can solve for X:
2X=a+a
2X=2a
Dividing both sides by 2 gives:
X=a
Conclusion
Thus, the single arithmetic mean between (a−b) and (a+b) is:
a
The two numbers given are:
- First number: a−b
- Second number: a+b
We denote the arithmetic mean by X. In an arithmetic progression (AP), the mean is the middle term, so we have:
- a−b,X,a+b
In an AP, the common difference between consecutive terms is constant. Therefore, we can express the common difference D in two ways:
1. From the first term to the mean:
D=X−(a−b)
2. From the mean to the second term:
D=(a+b)−X
Since both expressions represent the same common difference, we can set them equal to each other:
X−(a−b)=(a+b)−X
Now, we simplify the equation:
X−a+b=a+b−X
Adding X to both sides gives:
2X−a+b=a+b
Now, subtract b from both sides:
2X−a=a
Now, we can solve for X:
2X=a+a
2X=2a
Dividing both sides by 2 gives:
X=a
Thus, the single arithmetic mean between (a−b) and (a+b) is:
a
Similar Questions
Find the single arithmetic mean between: 7and31
View SolutionFind the single arithmetic mean between: 6and−18
View SolutionFind the arithmetic mean between 5 and 9.
View SolutionFind 4 arithmetic means between -5 and 15.
View SolutionFind the arithmetic mean of:
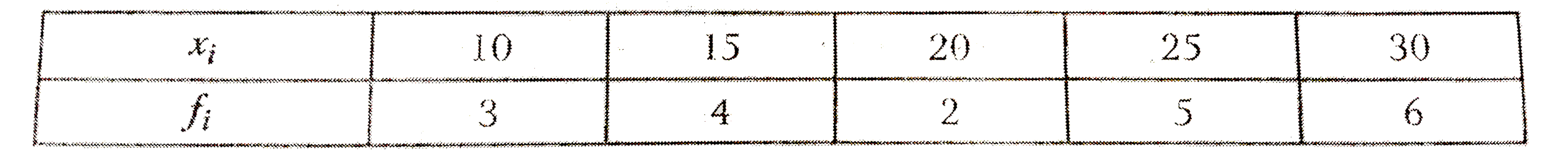
View SolutionFind the arithmetic mean between :
(i) 9 and 31
(ii) (m−n)and(m+n)
12 and - 22
View SolutionFind 6 arithmetic means between 8 and 29.
View SolutionFind 4 arithmetic means between 3 and 18.
View SolutionFind 7 arithmetic means between 6 and 46.
View SolutionInsert 4 arithmetic means between 3 and 23 .
View Solution
