The shaded region, where P=(−1,0),Q=(−1+√2,√2)R=(−1+√2,−√2),S=(1,0)
is represented by
Figure
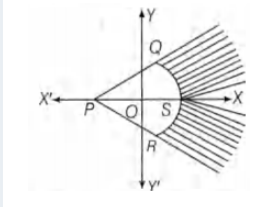
|z+1|>2,∣arg(z+1)<π4
|z+1|<2,∣arg(z+1)<π2
|z+1|>2,∣arg(z+1)>π4
|z+1|<2,∣arg(z+1)>π2
Step by step video & image solution for The shaded region, where P=(-1,0),Q=(-1+sqrt(2),sqrt(2))R=(-1+sqrt(2),-sqrt(2)),S=(1,0) is represented by Figure |z+1|gt2,|a r g(z+1)ltpi/4 |z+1|lt2,|a r g(z+1)ltpi/2 |z+1|gt2,|a r g(z+1)gtpi/4 |z+1|lt2,|a r g(z+1)gtpi/2 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The shaded region ,where P=(−1,0)Q=(−1+√2,√2)
R=(−1+√2,−√2),S=1(1,0) is represent by

View SolutionThe locus of z which lies in shaded region (excluding the boundaries) is best represented by Fig

View SolutionPlot the region represented by π3≤arg(z+1z−1)≤2π3 in the Argand plane.
View SolutionIf z(2−2√3i)2=i(√3+i)4, then arg(z)=
View Solutionif |z1+z2|=|z1|+|z2|, then prove that arg(z1)=arg(z2) if |z1−z2|=|z1|+|z2|, then prove that arg(z1)=arg(z2)=π
View SolutionProve that ∣∣∣z1−z21−¯z1z2∣∣∣<1if|z1|<1,|z2|<1
View SolutionIf |z|=1 and w=z−1z+1 (where z≠−1), then Re(w) is 0 (b) 1|z+1|2 ∣∣∣1z+1∣∣∣,1|z+1|2 (d) √2|z|1∣2
View SolutionFor any two complex numbers, z1,z2
∣∣∣12(z1+z2)+√z1z2∣∣∣+∣∣∣12(z1+z2)−√z1z2∣∣∣ is equal to
View SolutionIf z=(√32+12i)5+(√32−i2)5, then (a) im(z)=0 (b) Re(z)>0,Im(z)>0 (c) Re(z)>0,Im(z)<0 (d) Re(z)=3
View SolutionIf |z1|=|z2|=1, then prove that |z1+z2|= ∣∣∣1z1+1z2∣∣∣
View Solution
