If each element of as third order determinant of value is multiplied by 5 then value of the new determinant is
(A) B) (C)(D)
To solve the problem, we need to understand how the determinant of a matrix changes when we multiply each element of the matrix by a constant.
1. Understanding the Determinant:
Let the original determinant be represented as Δ. This determinant is of a third-order matrix (3x3).
2. Applying the Property of Determinants:
There is a property of determinants that states if each element of an n×n matrix is multiplied by a constant k, then the value of the determinant is multiplied by kn. Here, n is the order of the determinant.
3. Identifying the Values:
In our case:
- The constant k=5
- The order of the determinant n=3 (since it is a third-order determinant)
4. Calculating the New Determinant:
According to the property, the new determinant Δ′ can be calculated as:
Δ′=kn⋅Δ
Substituting the values we have:
Δ′=53⋅Δ
Δ′=125⋅Δ
5. Conclusion:
Therefore, the value of the new determinant is 125Δ.
Final Answer:
The value of the new determinant is 125Δ, which corresponds to option (A).
---
Let the original determinant be represented as Δ. This determinant is of a third-order matrix (3x3).
There is a property of determinants that states if each element of an n×n matrix is multiplied by a constant k, then the value of the determinant is multiplied by kn. Here, n is the order of the determinant.
In our case:
- The constant k=5
- The order of the determinant n=3 (since it is a third-order determinant)
According to the property, the new determinant Δ′ can be calculated as:
Δ′=kn⋅Δ
Substituting the values we have:
Δ′=53⋅Δ
Δ′=125⋅Δ
Therefore, the value of the new determinant is 125Δ.
The value of the new determinant is 125Δ, which corresponds to option (A).
Similar Questions
If every element of a third order determinant of value Det<a is multiplied by 5, then the value of new determinant, is
View SolutionIf D is determinant of order three of Δ is a determinant formed by the cofactors of determinant D: then
View SolutionA triangle whose one angle is more than 90∘ is called
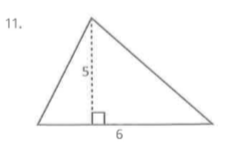
View SolutionDetermine the areas of the following triangles.
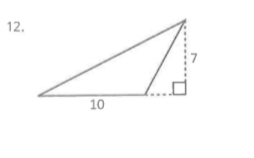
View SolutionDetermine the areas of the following triangles.
View SolutionThe sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
View SolutionThe sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
View SolutionThe sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
View SolutionThe sum of two equal angles of a triangle is equal to its third angle. Determine the measure of the third angle.
View SolutionTwo angles of a triangle are equal and the third angle is greater than each of those angles by 300 determine all the angles of the triangle.
View Solution
