In a test of 10 multiple of choice questions of one correct answer each having 4 alternative answers, the number of ways to put ticks at random for the answer to all the questions is
To solve the problem of finding the number of ways to put ticks at random for the answers to all 10 multiple choice questions, we can follow these steps:
1. Understanding the Problem: We have 10 multiple choice questions, and each question has 4 possible answers (A, B, C, D). We need to determine how many different ways we can answer all 10 questions.
2. Identifying Choices for Each Question: For each question, since there are 4 alternatives, we can choose any one of these 4 answers.
3. Calculating Total Combinations: Since the choice for each question is independent of the others, we can use the multiplication principle of counting. This means that for each question, we have 4 choices, and since there are 10 questions, the total number of ways to answer all questions is given by multiplying the number of choices for each question together.
Total ways=4×4×4×…(10 times)
This can be expressed using exponents:
Total ways=410
4. Final Calculation: Now we can compute 410.
410=1048576
Thus, the total number of ways to put ticks at random for the answers to all the questions is 1048576.
Final Answer:
The number of ways to put ticks at random for the answers to all the questions is 1048576.
---
The number of ways to put ticks at random for the answers to all the questions is 1048576.
Similar Questions
In an entrance test, there are multiple choice questions. There are four possible answers to each question, of which one is correct. The probability that a student knows the answer to a question is 90%. If the gets the correct answer to a question, then find the probability that he was guessing.
View SolutionIn an entrance test, there are multiple choice questions. There are four possible answers to each question, of which one is correct. The probability that a student knows the answer to a question is 90%. If the gets the correct answer to a question, then find the probability that he was guessing.
View Solution
Knowledge Check
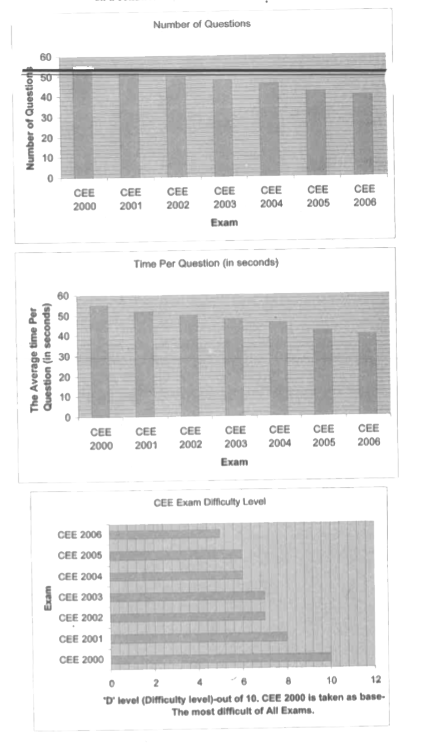
In which year were the test taker given the least time to answer all the questions?A2000B2001C2002D2006In a examination there are four multiple choice questions and each question has 4 choices. Number of ways in which a student can fail to get all answer correct is
(i) 256
(ii) 254
(iii) 255
(iv) 63A256B254C255D63
In a multiple choice question, there are four alternative answers of which one or more than one is correct A candidate will get marks on the question only if he ticks the correct answer. The candidate decides to tick answers at a random. If he is allowed up to three chances to answer the question, then find the probability that he will get marks on it.
View SolutionIn a multiple choice question, there are four alternative answers of which one or more than one is correct A candidate will get marks on the question only if he ticks the correct answer. The candidate decides to tick answers at a random. If he is allowed up to three chances to answer the question, then find the probability that he will get marks on it.
View SolutionIn a multiple choice question, there are five alternative answers of which one or more than one are correct. A candidate will get marks on the question, if he ticks all the correct answers. If he decides to tick answer all random, then the least number of choices should he be allowed, so that the probability of his getting marks on the question exceeds 18 is
View SolutionIn an examinations there are three multiple choice questions and each questions has 4 choices. Find the number of ways in which a student can fail to get all answer correct.
View SolutionA test paper has 20 multiple-choice questions. Each correct answer is awarded 3 marks but -2 marks are given for every wrong answer. No marks are awarded or deducted for questions that are not attempted.
a. Sia attempts all questions. She gets only 12 questions correct. How many marks did she score in this test?
b. Rajshree scores 5 marks in a test. If she answers 7 questions correctly, find the number of questions she did not answer correctly, and also the number of questions she did not attempt.
View SolutionA student has to answer 10 out of 13 questions in an examination. The number of ways in which he can answer if he must answer atleast 3 of the first five questions is 276 b. 267 c. 80 d. 1200
View Solution
